 図形問題の武器
図形問題の武器 ゼロから始める 図形の武器1 角度の問題の基礎
角度の問題の解き方。
まず自分で問題の「図をかいてみる」ことが重要。
問題に書いてある図を使うのではなく、自分で図を書き直し、問題を理解すること、これが一番重要です!
与えられた情報(条件)をすべて使うこと
これも...
 図形問題の武器
図形問題の武器 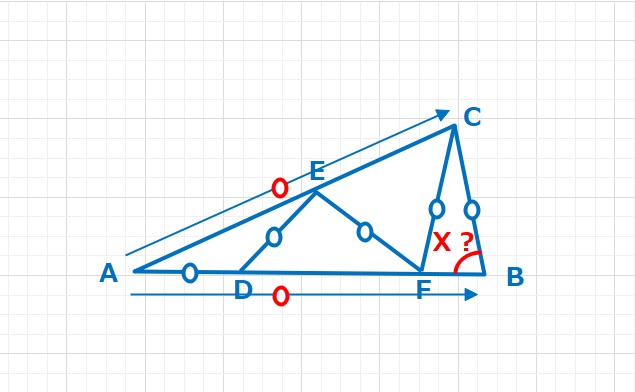 角度の問題
角度の問題  コラム
コラム 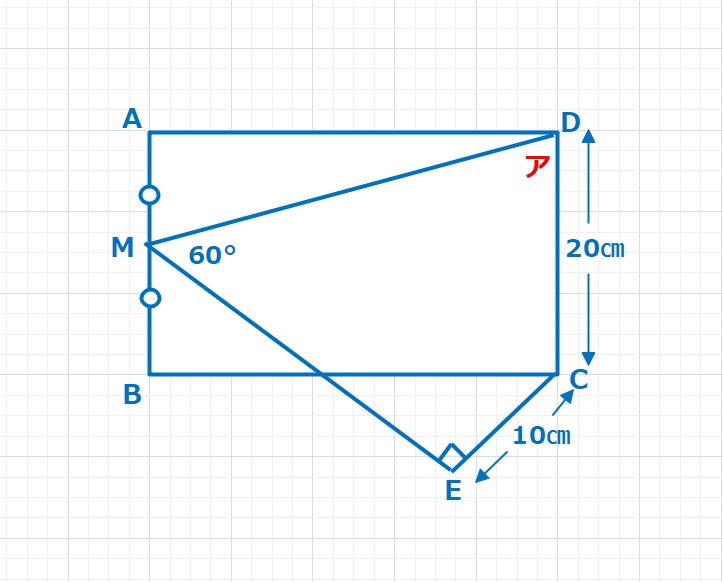 図形
図形 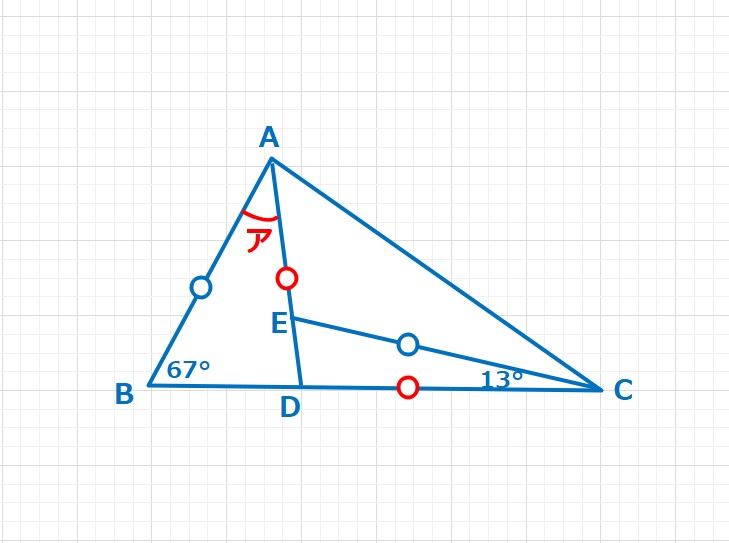 図形
図形 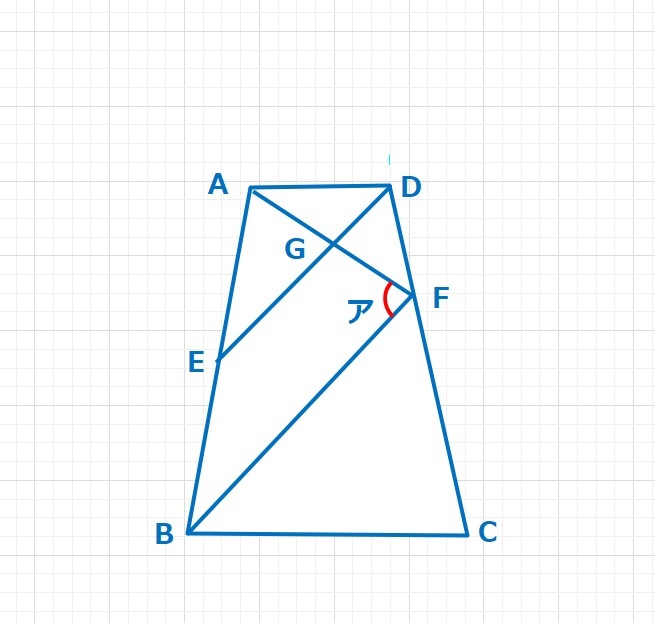 図形
図形 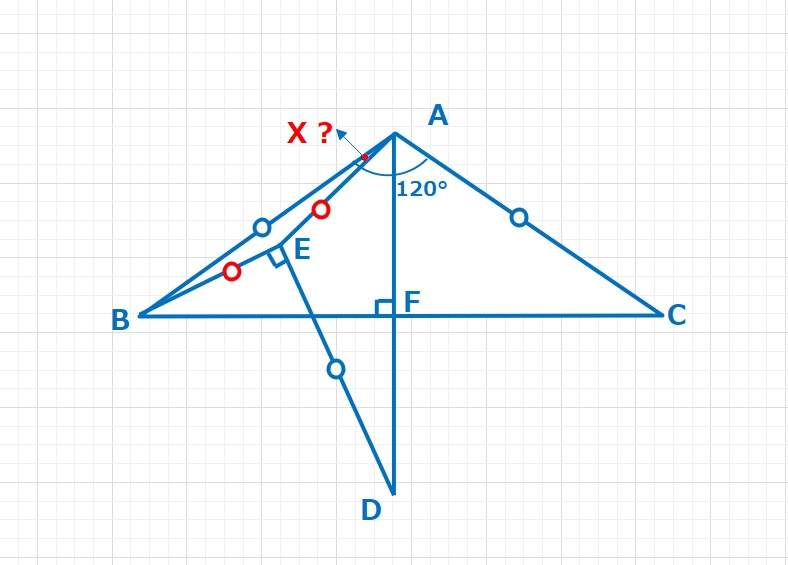 図形
図形 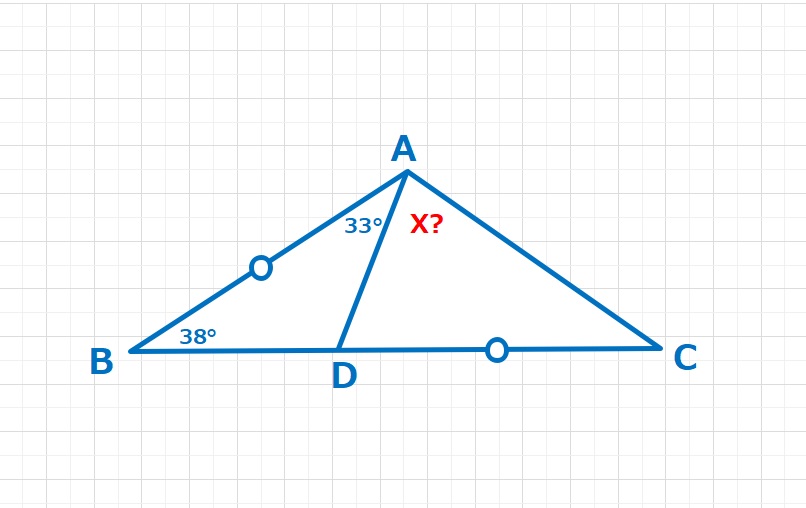 図形
図形 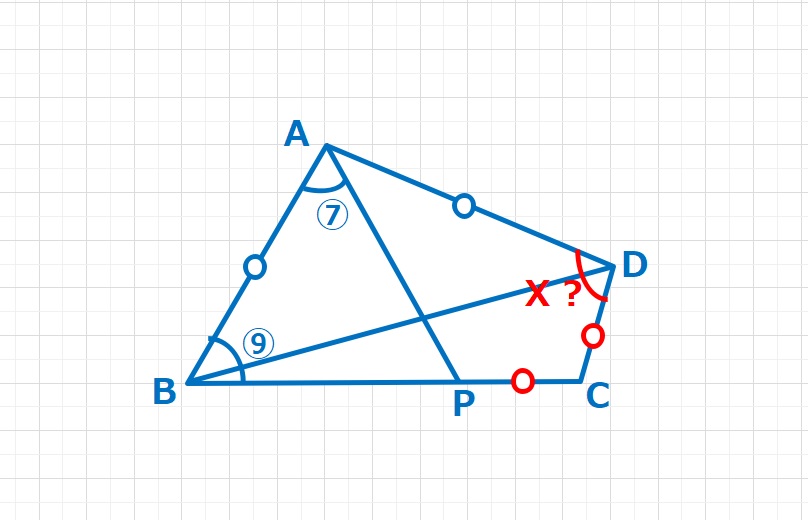 図形
図形 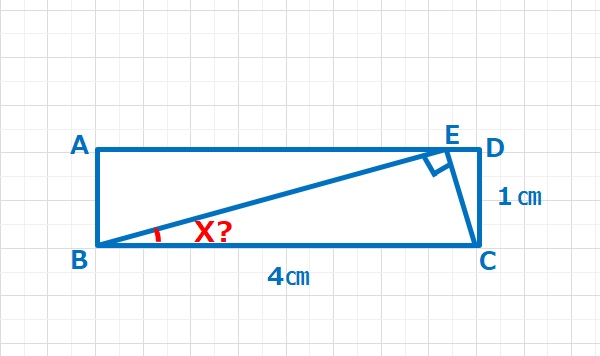 図形
図形 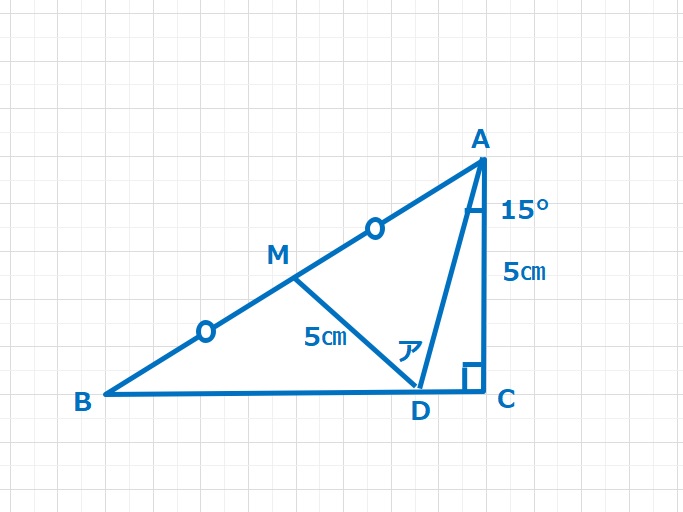 図形
図形 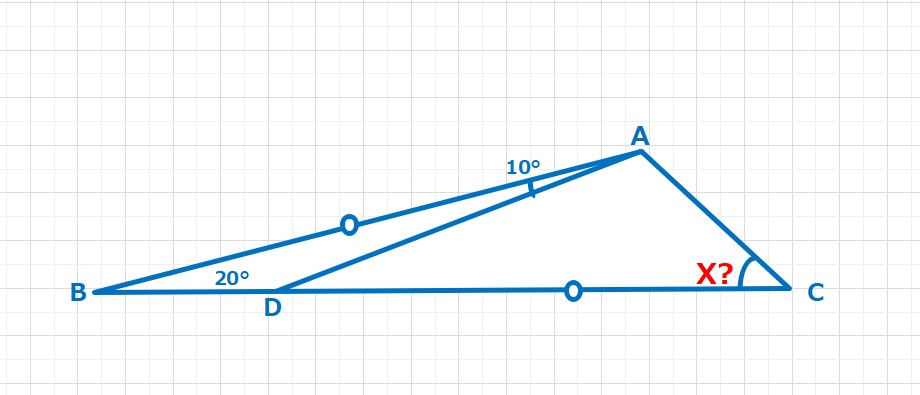 図形
図形 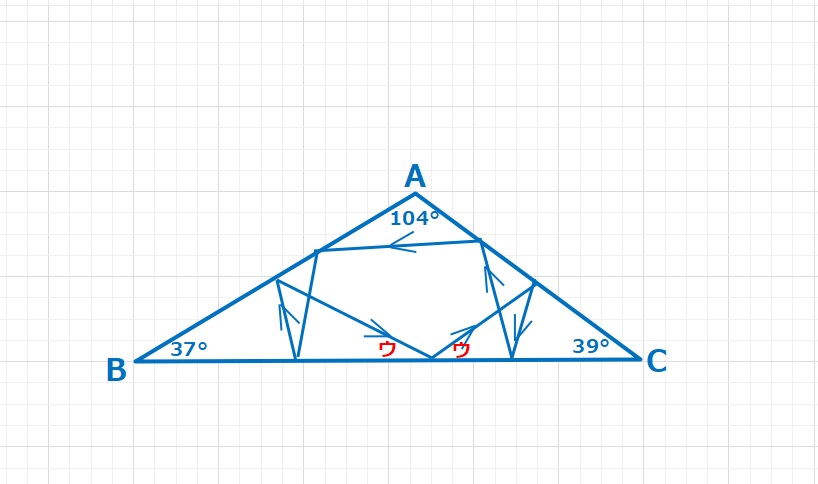 図形
図形 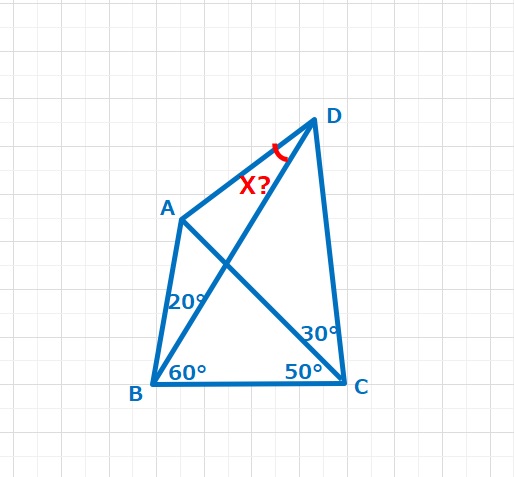 ラングレーの問題
ラングレーの問題 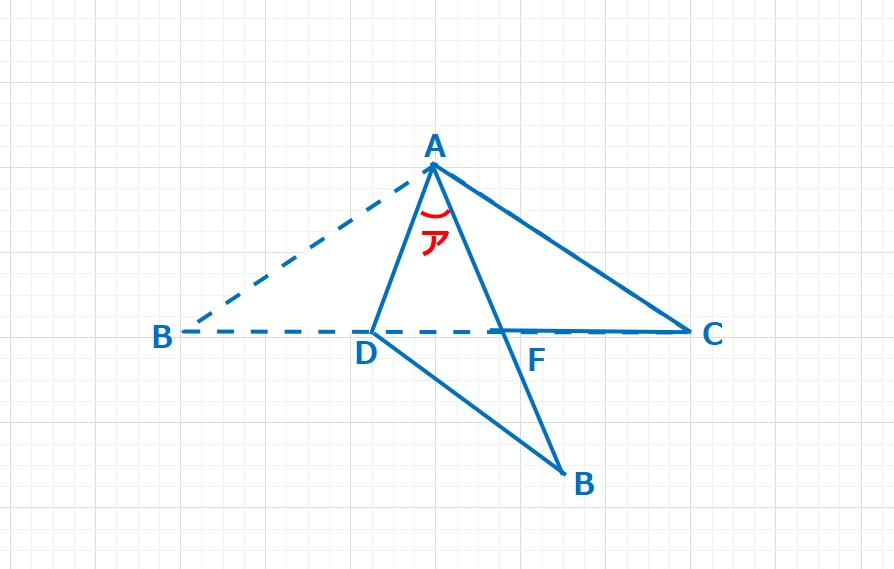 図形
図形 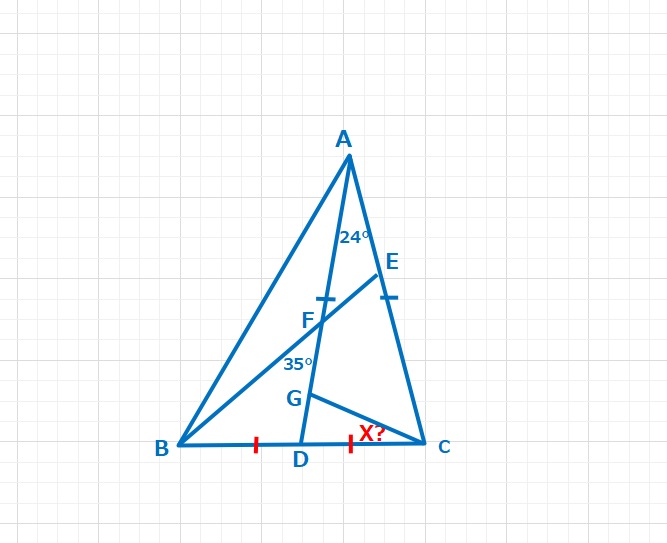 図形
図形 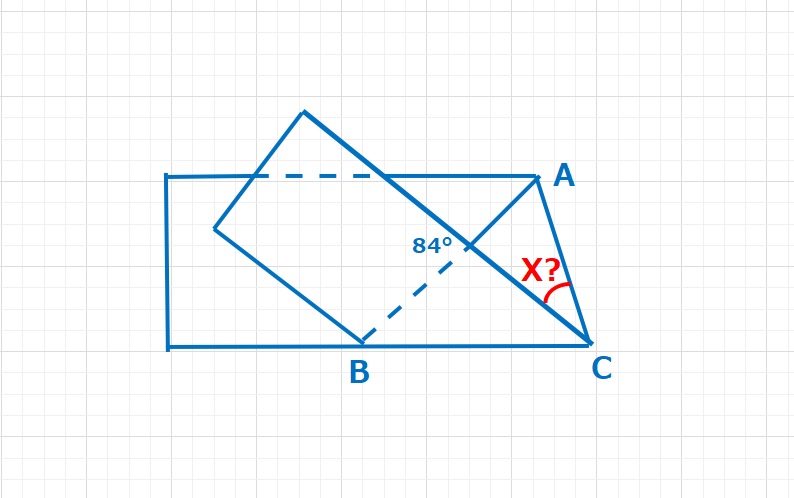 図形
図形 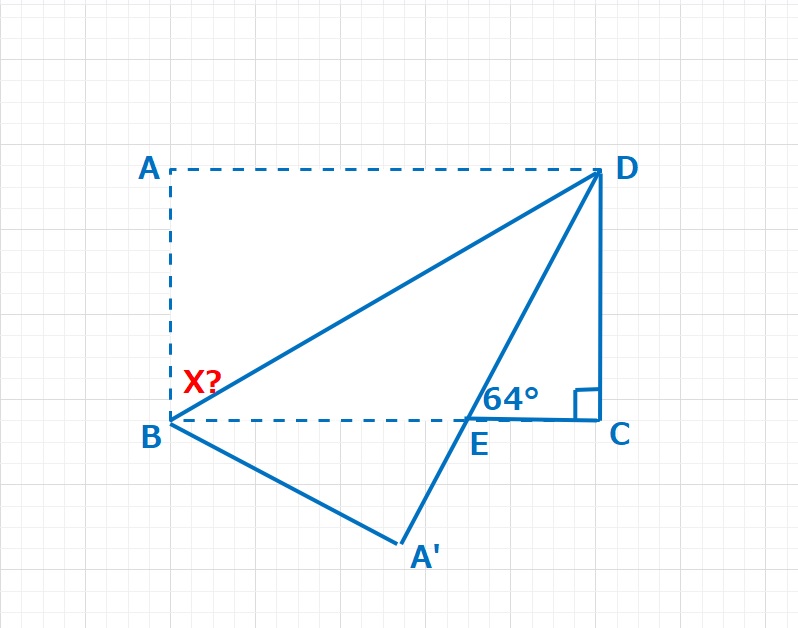 図形
図形 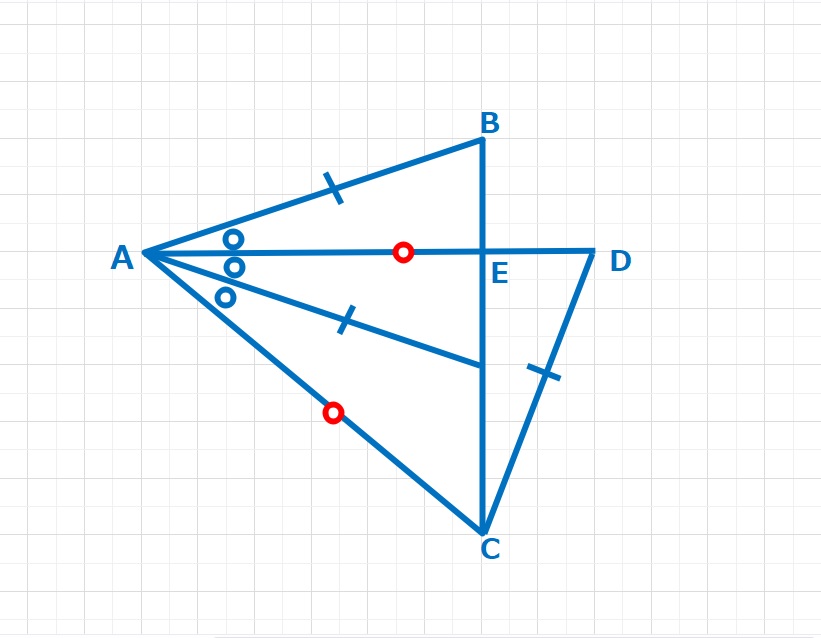 図形
図形 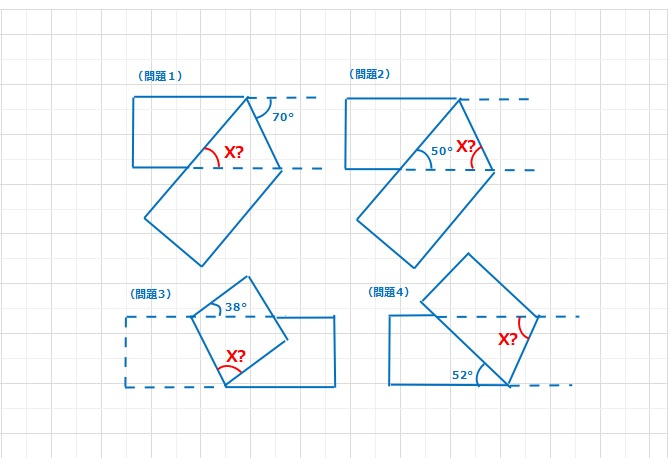 図形
図形