2023年 灘中入試問題1日目⑪番より
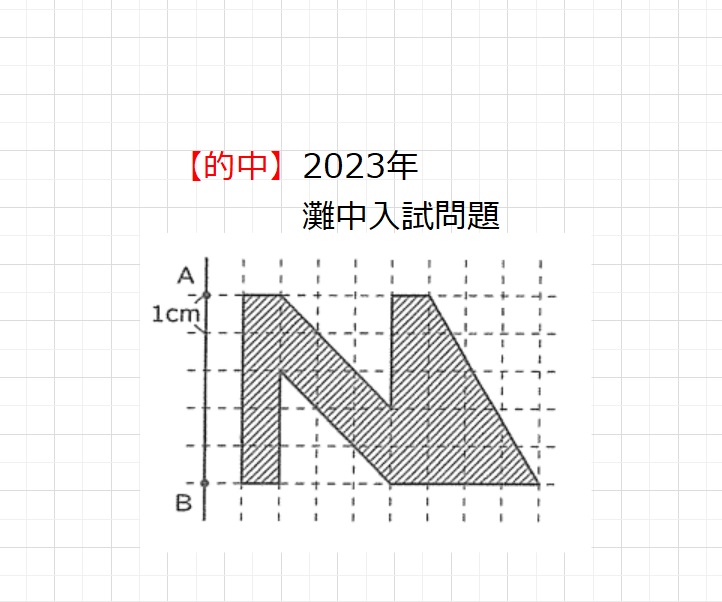
【問題】図のような、1目盛りの幅が1㎝の方眼用紙があります。斜線部分の図形を、2点A,Bを通る直線の周りに一回転させたとき、その図形が通過する部分の体積はア㎠です。
【ヒント】
そろそろ出そうな気がして、1月10日に関連問題を掲載させていただきました(笑)
ゼロから始める 図形問題の武器10 パップス・ギュルダンの定理 | 算数コロシアム (mathcolo.com)
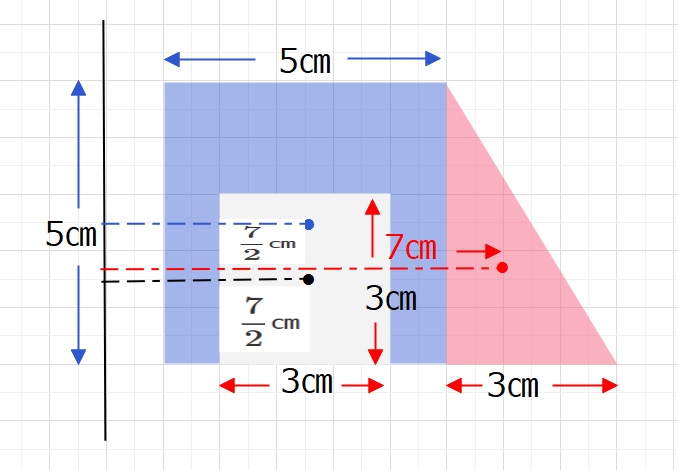
問題の図形は下の図のように変形できます。
求める体積は青い図形の面積に、半径\(\displaystyle\frac{7}{2}\)㎝の円周を掛けたものと、赤い面積に、半径7㎝の円周をかけたものになります。
【解答】
青の部分の回転した体積は
(青の正方形ー白の正方形)×2×\(\displaystyle\frac{7}{2}\)×3.14
=(25-9)×7×3.14=112×3.14
(赤の部分を開店した体積)=\(\displaystyle\frac{3×5}{2}\)×2×7×3.14
=15×7×3.14=105×3.14
よって求める面積は=(112+105)×3.14=217×3.14=681.38㎠・・・(答え)
【おまけ】
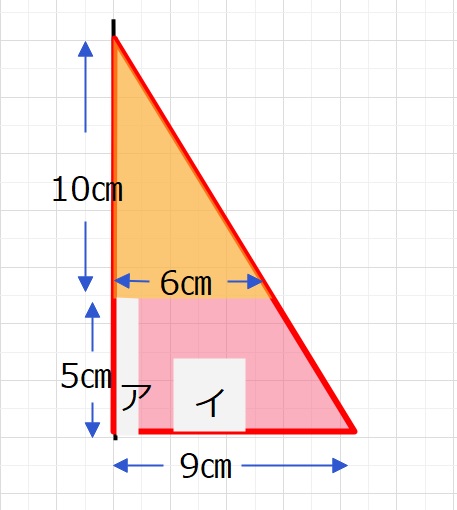
普通に解くと、(赤い直角三角形を回転させた円すい)-(オレンジ回転円すい)
から、アとイの回転体をさらにひきます。
赤回転の円すい=9×9×3.14×15×\(\displaystyle\frac{1}{3}\) =405×3.14
オレンジ回転円すい=6×6×3.14×10×\(\displaystyle\frac{1}{3}\)=120×3.14
アの回転体=1×1×3.14×5=5×3.14
イの回転体=(5×5-2×2)×3.14×3=63×3.14
求める体積は (405-120-5-63)×3.14=217×3.14=681.38㎠・・・(答え)

コメント