難易度
2017年 早稲田中入試より
【ヒント】
△AGDとAD=ABに注目して、△AGDをADがABに重なるように移動させ、
できた三角形を△AEBとします。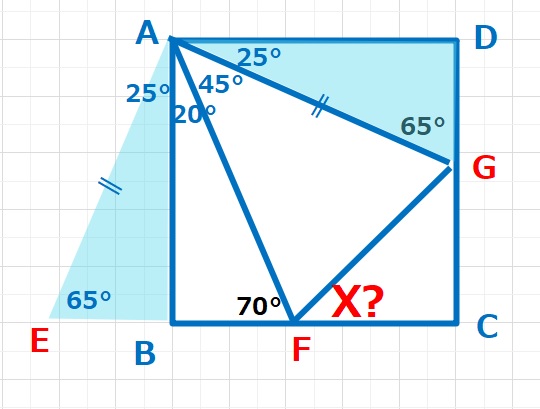
【解答】
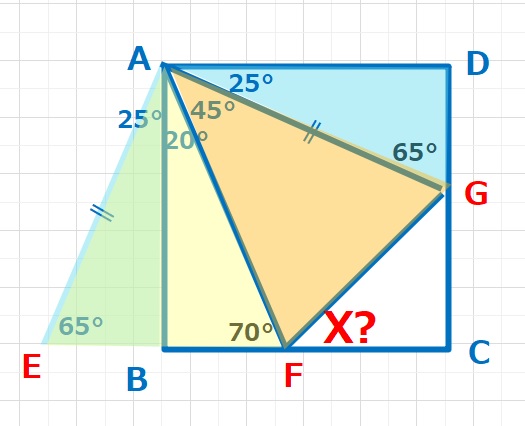
△AGDを△AEDとなるように移動すると、
△AEF(黄色)と△AGFは2辺(AF=AG,AF共通)とその間の角
(∠EAF=∠GAF=45°)が等しいので、合同な三角形となります。
よって∠AFG=∠AFE=70°
X=180-(70+70)=40°・・・(答え)
 図形
図形難易度
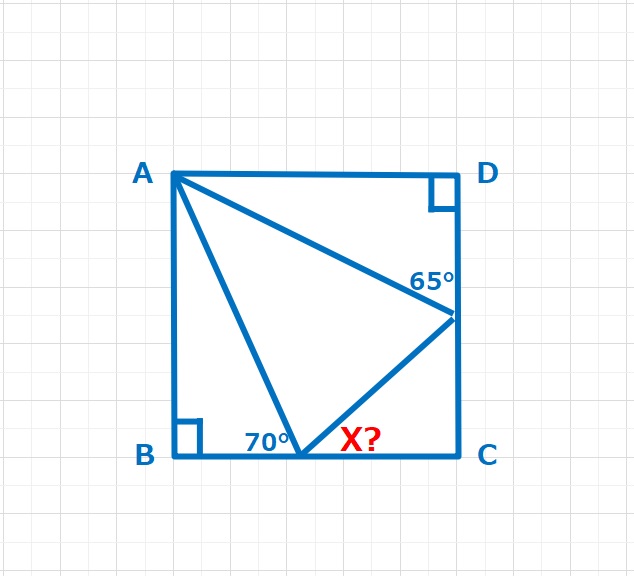
2017年 早稲田中入試より
【ヒント】
△AGDとAD=ABに注目して、△AGDをADがABに重なるように移動させ、
できた三角形を△AEBとします。
【解答】
△AGDを△AEDとなるように移動すると、
△AEF(黄色)と△AGFは2辺(AF=AG,AF共通)とその間の角
(∠EAF=∠GAF=45°)が等しいので、合同な三角形となります。
よって∠AFG=∠AFE=70°
X=180-(70+70)=40°・・・(答え)

コメント