難易度
2012年 ジュニア算数オリンピック ファイナル問題
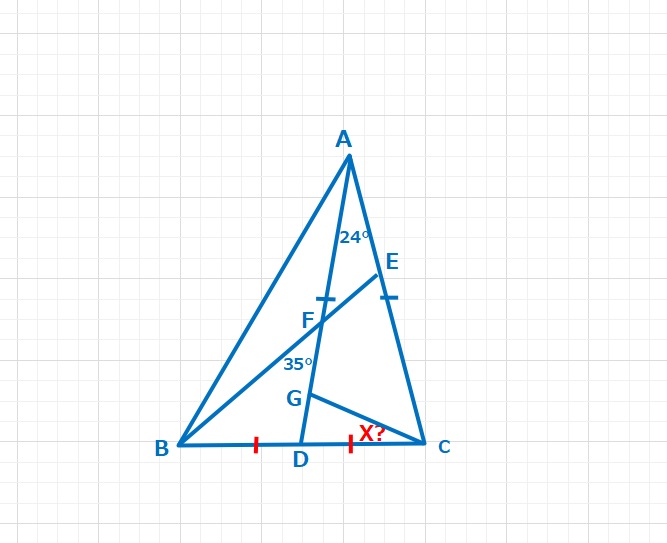
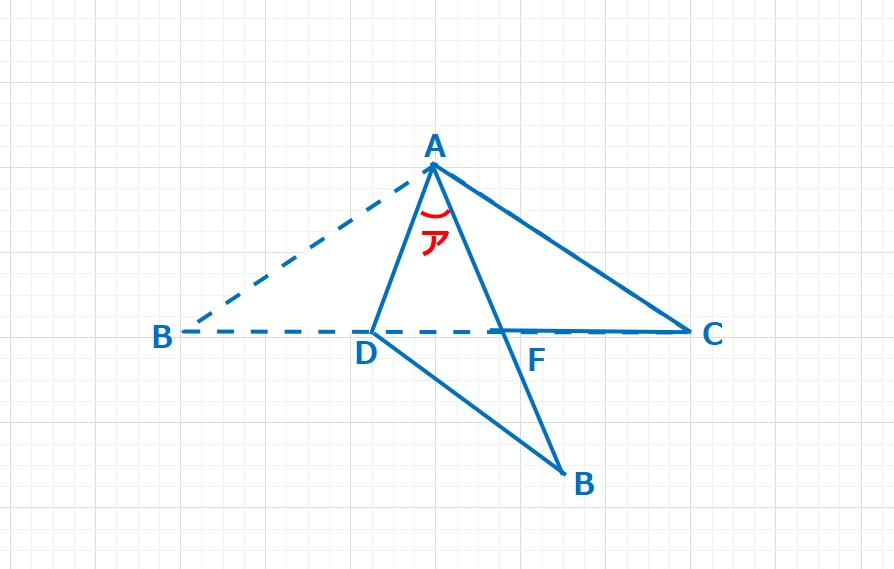
【問題】図において、BD=DC,AD=AC,BF=DF+DGとなっているとき、∠DCGは何度でしょうか。
【ヒント】算数の問題を解く鉄則は、当然ですが「与えられた条件をすべて使うこと」です。まずAD=ACより△ADCは二等辺三角形なので、∠ADC=∠ACD=\(\displaystyle\frac{180-24}{2}\)=78°となります。BF=DF+DGの条件が使いにくいですが、図のようにDGと同じ長さをDGの延長線上にGと反対側にDG’をとります。そうするとBF=DG’となり、△FBG’は二等辺三角形になります。
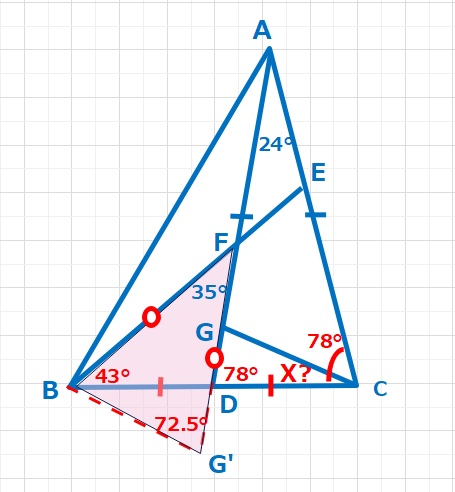
【解答】△FBG’は二等辺三角形なので、∠FBG’=∠FG’B=\(\displaystyle\frac{180-35}=72.5°
また、△DGCと△DG’Bにおいて二辺(GD=G’D,DC=DB)とその間の角(∠GDC=∠G’DB)が等しいので、合同な三角形となります。よって∠DCG=∠DBG’=72.5-43=29.5°・・・(答え)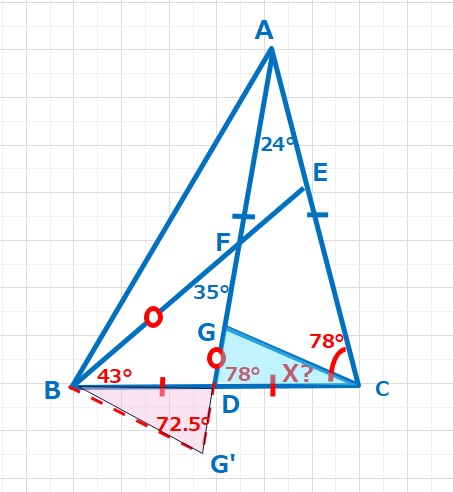
コメント