難易度
2018年 算数オリンピック ファイナル問題
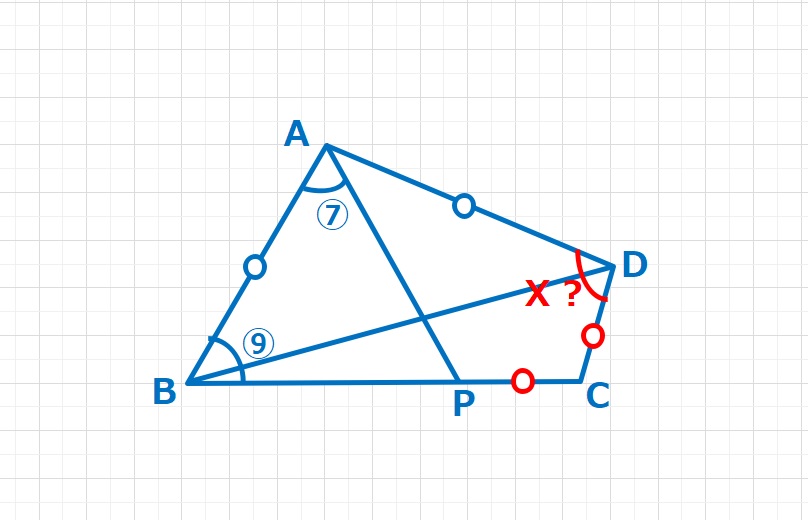
【問題】AB=ADかつ∠ABC+∠ADC=180°であるような四角形ABCDにおいて、辺BC上にCP=CDとなるように点Pをとると、角ABP:角BAP=9:7となった。Xの角度は何度ですか。
【ヒント1】∠ABP+∠ADC=180°,AB=ADに注目して、△ADCを△ABQに移動させます。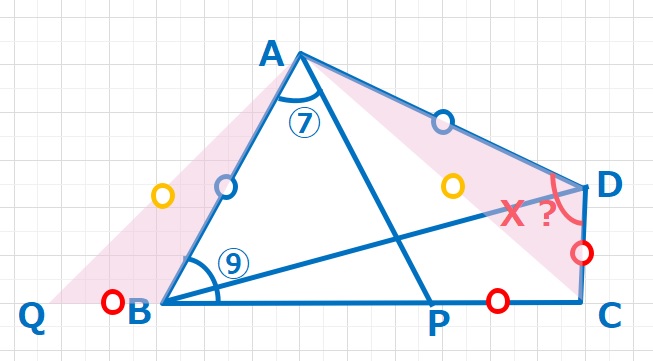
【ヒント2】△AQBと△ACPにおいて、2辺(AQ=AC,QB=CP)とその間の角(△AQCが二等辺三角形なので∠AQB=∠ACP)が等しく、合同な三角形となります。よってAB=APとなり、△ABPも二等辺三角形となります。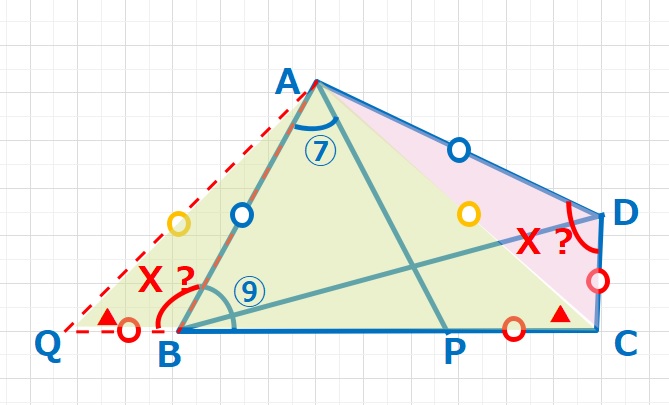
【解答】△ABPは二等辺三角形なので、∠ABP=∠APB=⑨、△ABPの内角の和は180°なので、⑦+⑨+⑨=180°となり、①=\(\displaystyle\frac{180}{25}\)=7.2°となります。また、△ABQと△APCは合同な三角形なので求めるXは①が16個ぶんですので、
7.2×16=115.2°・・・(答え)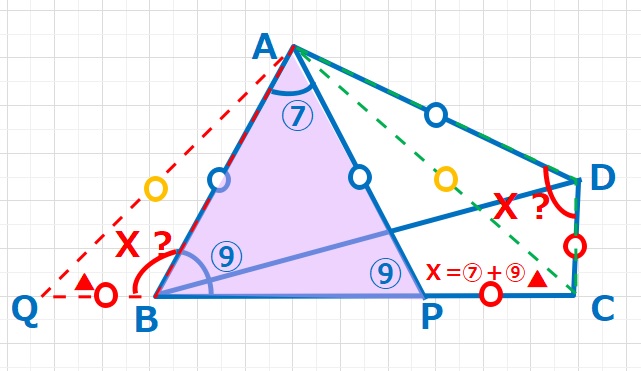
おまけ
中学生で習う知識を使うと、∠ABC+∠ADC=180°より、四角形ABCDは円に内接していることがわかります。また∠ABD=∠ACD, ∠ADB=∠ACBで、かつ△ABDは二等辺三角形なので、∠ABD=∠ADBなため、∠DCA=∠PCAがわかります。また、CD=CPなので、四角形ADCPはたこ型四角形(∠CRD=∠CRP=90°)となり、X=∠ADC=∠APC=∠ABC+∠BAPとなります。よって、7.2×16=115.2°・・・(答え)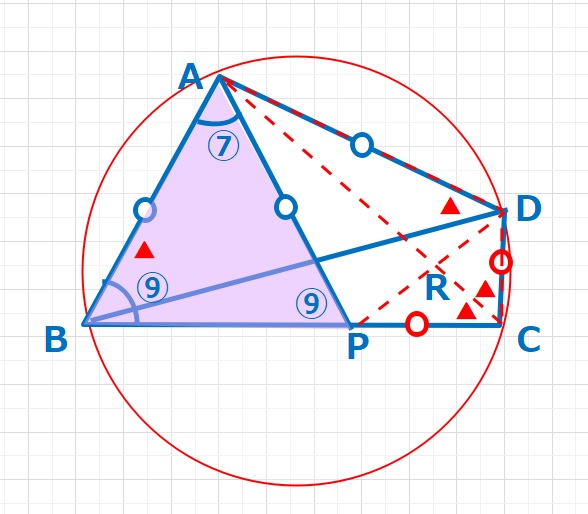
コメント