角度の問題の解き方。
まず自分で問題の「図をかいてみる」ことが重要。
問題に書いてある図を使うのではなく、自分で図を書き直し、問題を理解すること、これが一番重要です!
与えられた情報(条件)をすべて使うこと
これも当たり前と思うかもですが、試験問題で必要のない情報というものは基本書いてません。与えられた情報を1つ1つ確認し、すべて使い切りましょう。
与えられた情報から、あらたにわかる情報をすべて書き込んでいく。
対頂角は等しい
下図のアとイ,ウとエのように対にあたる角どおしを対頂角といい、その大きさは等しくなります。
感覚てきにわかると思いますが、簡単に説明します。アとウを足すと180°になります。またウとイをたすとこれも180°になります。よって、ア+ウ=ウ+イとなり、ア=イが成り立ちます。ウ=エに関しても同様です。
2つの直線が平行なとき、同位角・さっ角は等しい。
図のような、アとA,イとB,ウとC,エとDのように同じ位置にある関係を同位角といいます。2つの直線が平行なとき、同位角は等しくなります。
また2つの直線があるとき、鏡越しに反転するような関係の角、例えばエとA,ウとBのような関係を錯角といい、2つの直線が平行なとき、錯角は等しくなります。上の対頂角と同位角の性質を使えば、自動的に理解できると思います。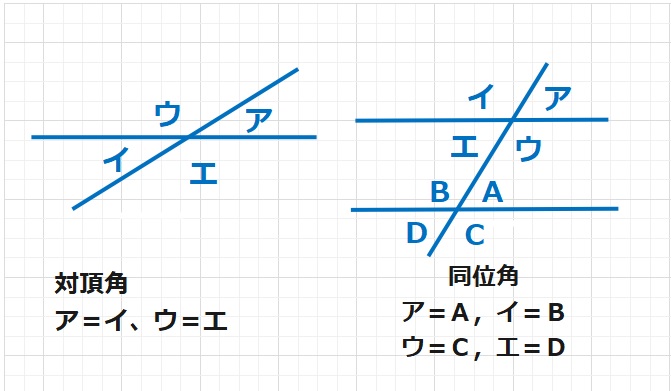
三角形の外角の関係を使う
下の図のアやイ,ウにあたる角を三角形の内角といい、エ,オ,カにあたる角を三角形の外角といいますが、アとイの合計はエになります。これを式で表すと、ア+イ=エと表現でき、言葉で書くと「三角形の1つの外角は、となりあわない2つの内角の和に等しい」と少し難しい表現になります。
これは知らなくても問題ないのですが、これを使うことによって計算が簡単になるため、試験の際に時間短縮となります。簡単に説明すると、三角形の内角の和は180°なのでア+イ+ウ=180°。またウとエは一直線となっているため、ウ+エ=180°。よってア+イ+ウ=ウ+エとなり、ア+イ=エが成り立ちます。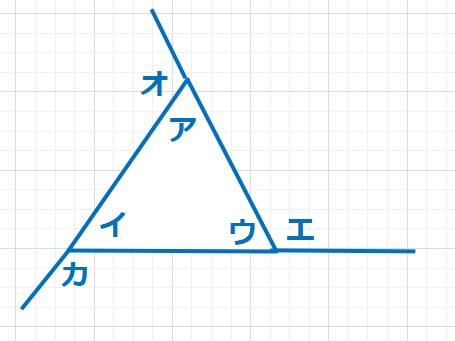
三角形の合同を使う、対称な図形・相似な図形を探す
2つの三角形があるとき、合同である条件は3パターンあります。
・3組の辺の長さが等しい(これを格好よく言うと、3辺相当といいます)
・2辺とその間の角が等しい(これを格好よく言うと、二辺夾角相当といいます)
・2角のその間の辺が等しい(これを格好よく言うと、二角夾辺相当といいます)
この3つのうちのいずれかの条件を満たしたとき、△アイウと△ABCは合同といい、△アイウ≡△ABCと記号で書きます。合同な三角形は、当然 ∠ア=∠A,∠イ=∠B,∠ウ=∠Cが言えます。
ただし、3つの角が等しいからといって三角形が合同であるとは限りません。
対象な図形・相似な図形に関しては、改めて「図形の武器」の別の項目で説明します。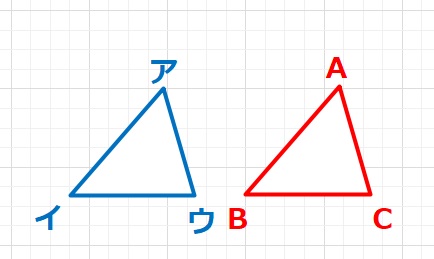
特殊な図形の性質を使う。
この項目に関しては、改めて「図形の武器」の別の項目で説明します。
・正三角形、二等辺三角形、
「45°,45°,90°」、「30°,60°,90°」の直角三角形の性質。
・四角形 ー正方形,長方形,ひし形,平行四辺形,等脚台形,たこ形四角形ーの性質。
・正五角形の性質。
などが、よく使う図形の性質となります。
コメント