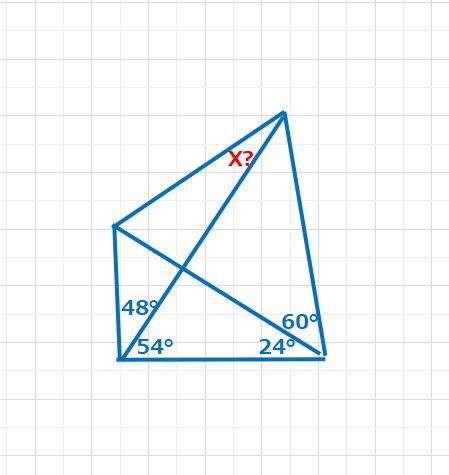
難易度 L(48,54,24,60)
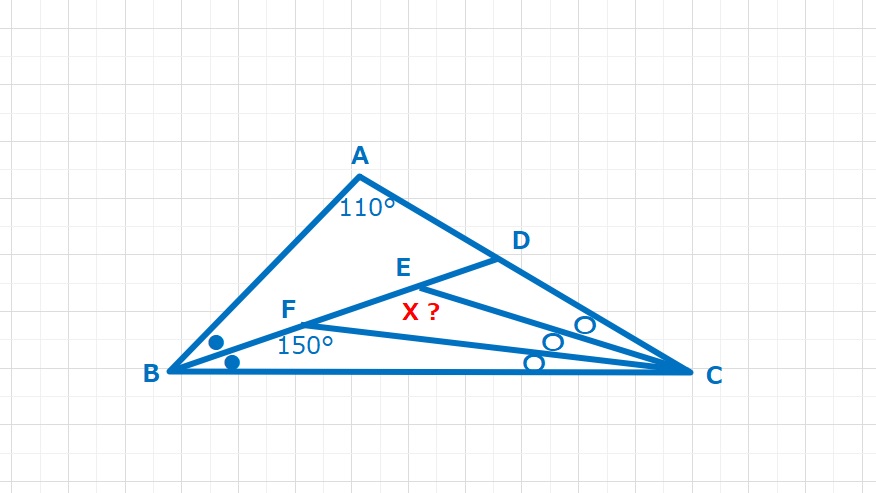
【問題】Xの大きさは何度ですか。
6の倍数の角度の問題は「例の図形」を思いだす。
【ヒント1】60°があり、一見簡単そうにみえますが、なかなかうまくいきません。
唯一の糸口は与えられた数字、48,54,24,60がすべて6の倍数であること。といえば、例のあの形を使いたくなります。しかし、6の倍数でも特徴的な108や72,36という数字がないため使えるかどうか不安もあります。いきなり答えをみるともったいないので、底辺10㎝くらいの大きさで、いちど分度器と定規で実際に問題を作図して、じっくり眺めていただきたいです。(笑)
【ヒント2】こんな感じの補助線が近道であると思います。もっと簡単な方法があればお教えください。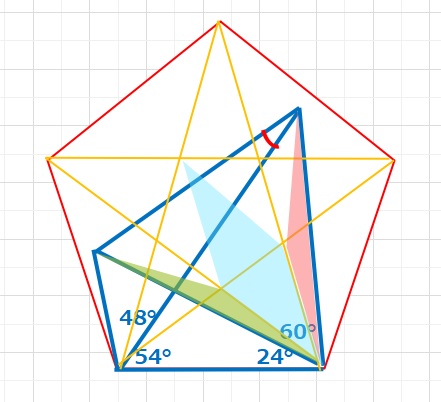
【解答】BCを1辺とする正五角形を点Aと同じ側に下図のようにとり、各点にA,B,C,D,E,F,G,Hと記号をふります。
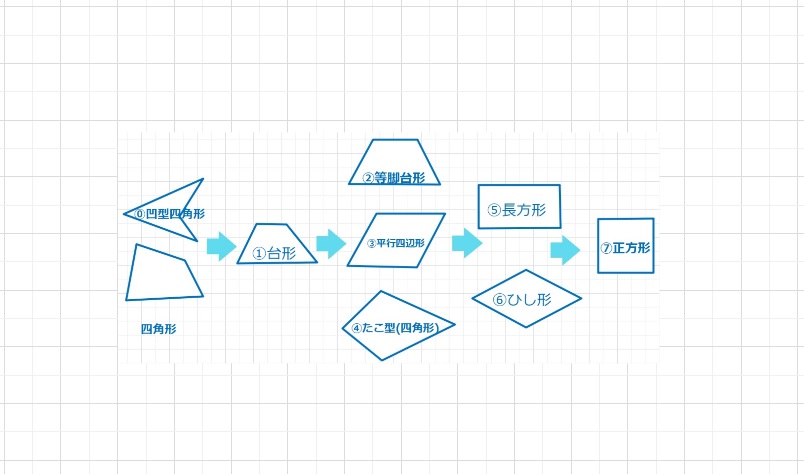
・四角形DECFについて、正五角形の性質より∠EDF=∠ECF=36°,∠DFC=∠DEC=104°となり、四角形DECFはひし形となります。
・△ECBについて、∠ECB=∠EBC=36°なので△ECBはEC=EBの二等辺三角形となる
・△FCHについて、∠FCH=∠FHC=36°なので△FCHはFC=FHの二等辺三角形となる
ここで、DEを一辺とする正三角形DXEをとると、△EXCについて∠XEC=180-24=156°なので∠CXE=12°となり、∠CXE=∠XCE=12°で△EXCはEX=ECの二等辺三角形となる
△EXBはEX=EBの二等辺三角形なので、∠EXB=∠EBX=\(\frac{180-48}{2}\)=66°
よって∠XBC=66+36=102°となり、これは今回の問題で与えられた点をGとすると、これと一致します。
・同様にDFを一辺とする正三角形DFYをとると、この点は今回の問題で与えられた点をAとすると、Yはこの点と一致します。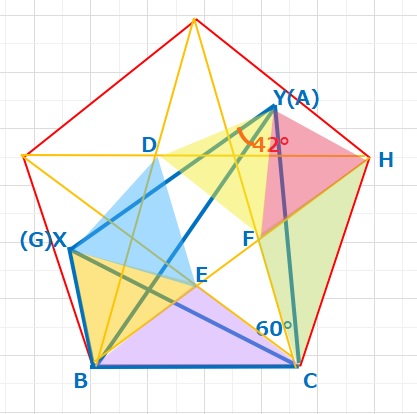
以上をふまえると、△EGCと△FACは2辺(EG=FA,EC=FC)とその間の角(∠GEC=∠AFC=156°)が等しいので合同な三角形となります。よって△AGCは正三角形となります。
X=∠GAB=∠GAC-∠BAC=60-42=18°・・・(答え)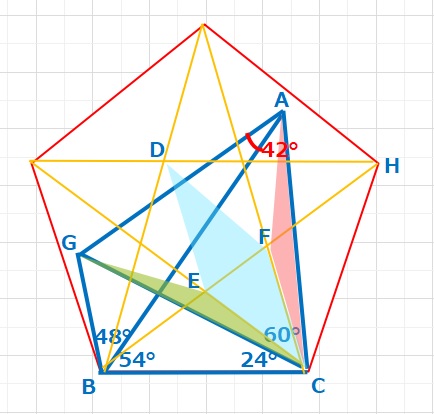
コメント