三角形の外角の関係から導いた裏ワザ LV1
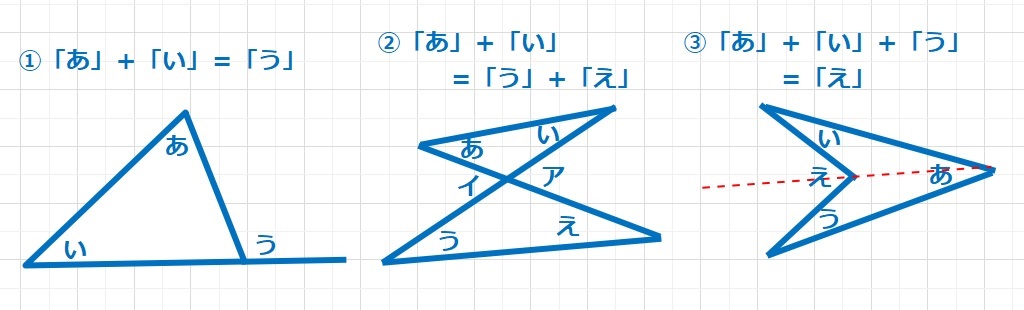
①は三角形の内角の和が180°であることから簡単に導くことができます。
②は①の応用で「あ」+「い」=「ア」となり、「う」+「え」=「イ」となります。
同位角は等しいので「ア」=「イ」ですので、「あ」+「い」=「う」+「え」となります。
蝶々の右はねの合計と左はねの合計は等しくなります(笑)
③は赤の点線をいれて上と下で三角形を2つ作ります。これも三角形の外角の関係で「い」と「あ」の上半分の合計は「え」の上半分となります。また「う」と「あ」の下半分の合計は「え」の下半分となります。ということは、「あ」+「い」+「う」=「え」ということです。
三角形の外角の関係から導いた裏ワザ LV2
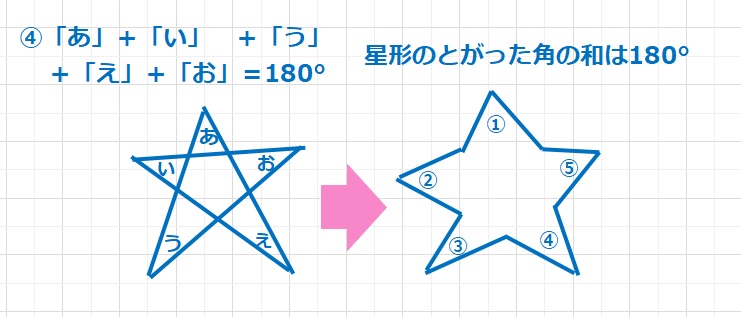
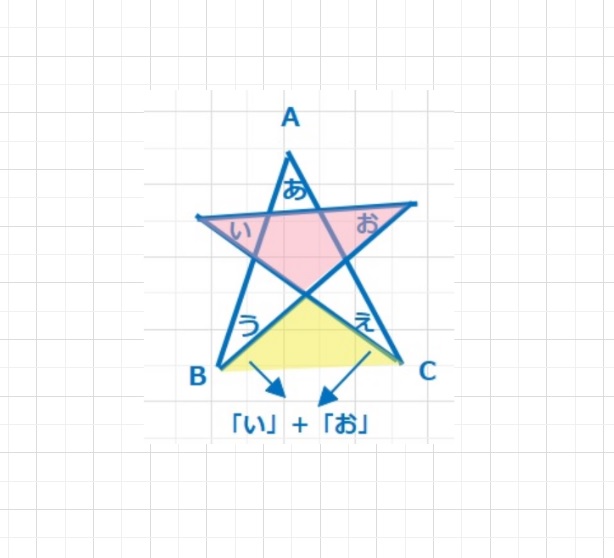
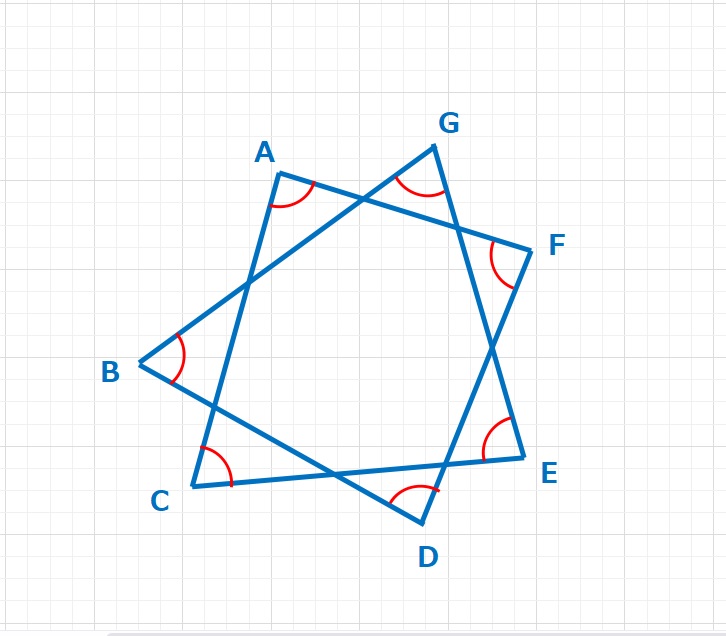
一筆書きでかける星形のとがった角の和は180°になります。その発展で右図のような星形のとがった角の和も180°になります。これはLV1の蝶々形を使うとすぐに理解できます。三角形の外角の関係をもちいても導くことができます。
下図のように赤と黄色を蝶々の羽だと思うと、「い」+「お」は黄色のしたに移動できます。そうすると、求める角度は△ABCの内角の和、180°となります。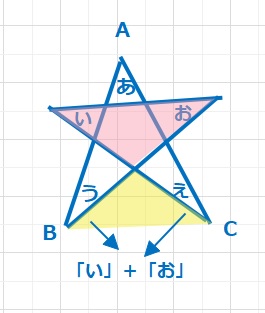
三角形の角度の裏ワザ LV3
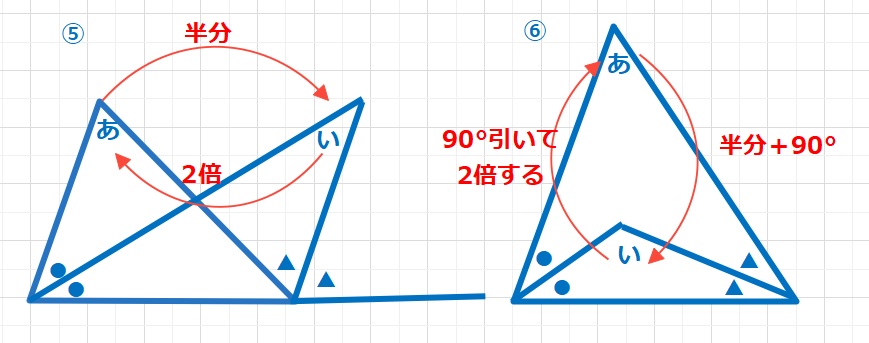
⑤中学で詳しく習うことかと思います。三角形の外角の関係から、
▲▲=●●+「あ」・・・(1)が成り立ちます。
又、▲=●+「い」も成り立ちますので、▲▲=●●+「い」+「い」・・・(2)
(2)から(1)を引くと、0=「い」×2-「あ」となり、
「あ」=「い」×2となります。逆に「い」=「あ」×\(\frac{1}{2}\)となります。
⑥については、三角形の内角の和より、
●+▲+「い」=180・・・(3)が成り立ちます。
又、●●+▲▲+「あ」=180・・・(4)も成り立ちます。
(3)より ●●+▲▲+「い」×2=360・・・(5)となり、
(5)から(4)を引くと、「い」×2ー「あ」=180となります。
つまり、「あ」=「い」×2-180=2×(「い」-90)となり、「あ」は「い」から90を引いて2倍することになります。同様に、「い」=(「あ」+180)×\(\frac{1}{2}\)=90+「あ」×\(\frac{1}{2}\)となり、「い」は「あ」を2倍して90足すことになります。
少し、わかりにくいかもですね。
コメント