難易度
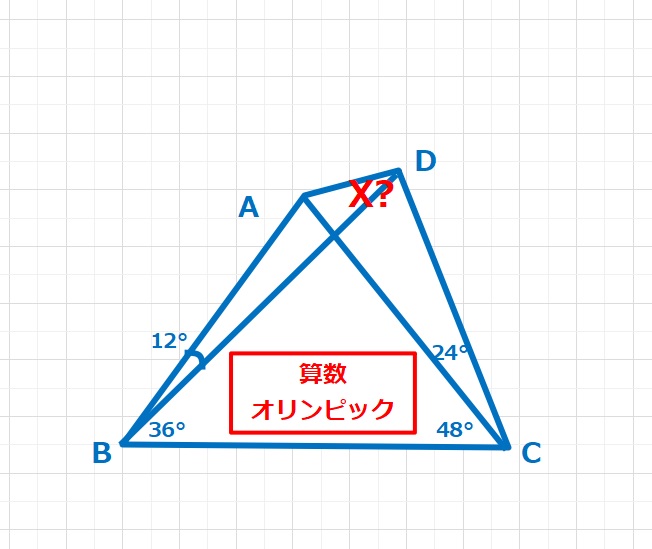
L(12,36,48,24)
算数オリンピック出題問題
【ヒント】
ラングレーの角度の問題では、対称性などを考え、隠された正三角形や二等辺三角形
をみつけることによって、簡単に解くことができます。
△ABCは∠ABC=∠ACB=48°なので二等辺三角形となります。
BCを底辺とする正三角形をつくってみます。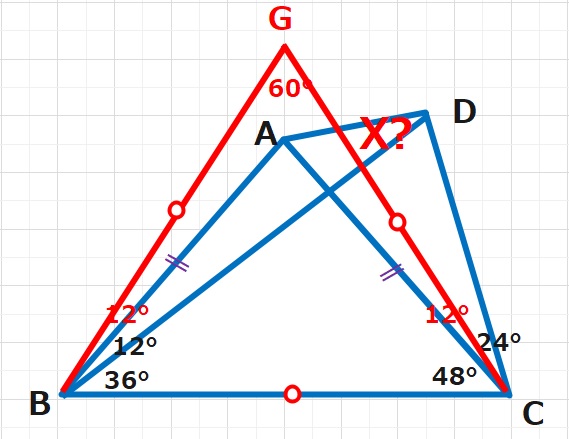
【解答】
△ABCは∠ABC=∠ACB=48°の二等辺三角形なのでAB=AC
△BCDは∠BCD=∠BDC=72°の二等辺三角形なのでBC=BD
BCを底辺とする正三角形GBCを作ると GB=BC=GCとなり、
BG=BDなので△BGAと△BDAは二辺とその間の角が等しく合同な三角形となる。
X =∠ADB=∠AGB=\(\displaystyle\frac{60}{2 }\) =30°
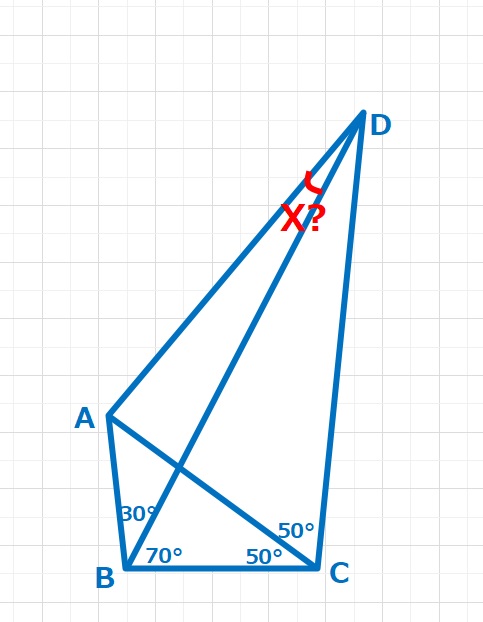
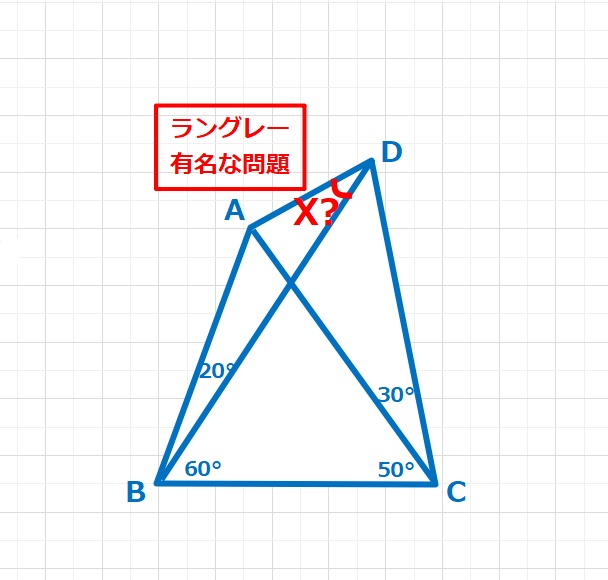
コメント