この問題は、The Mathematical Gazette誌1922年10月号に掲載され、反響が大きく、翌1923年5月号で、読者からの投稿による7通りの解法が掲載され、三角関数を用いたものが3通り、初等幾何を用いた解法が4通り紹介されたそうです。斉藤 浩著「ラングレーの問題にトドメをさす!」より。
難易度
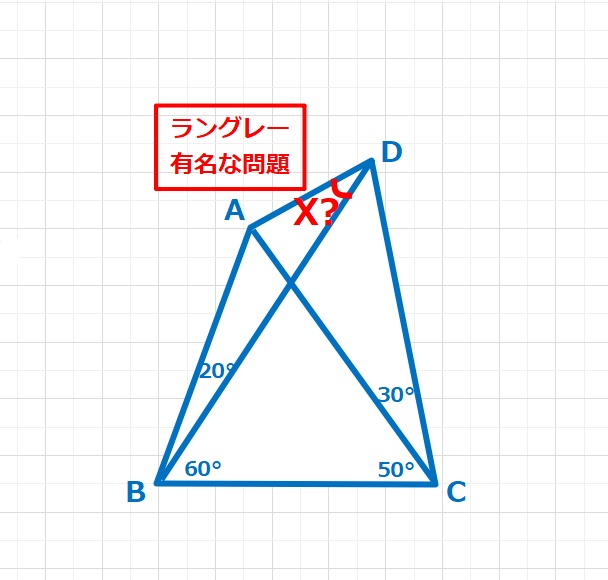
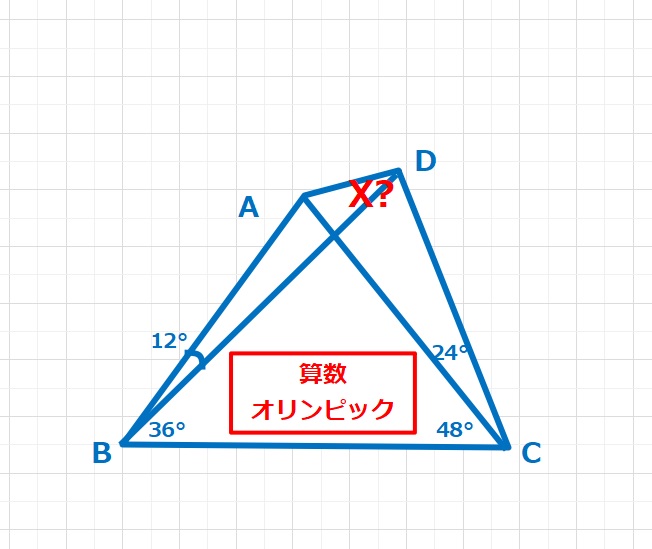
L(20,60,50,30)
【ヒント】BD=BFとなるFをとり、またED=EGとなるGをDFの延長線上にとります。 △BDFは二等辺三角形、△EDGは正三角形となります。
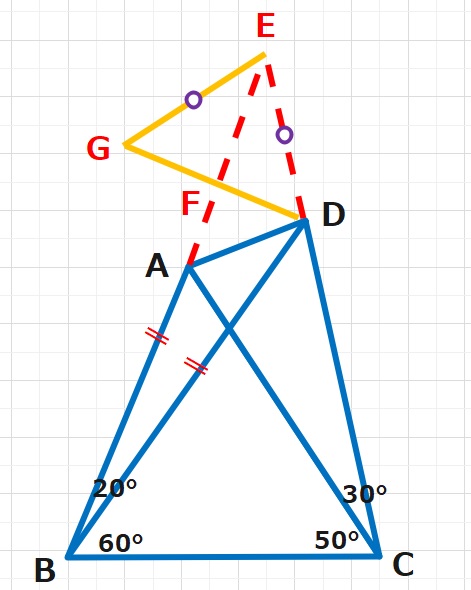
【解答】図が正確でないため少し違和感があります。BD=BFとなるFをとり、またED=EGとなるGをDFの延長線上にとります。△BDFは二等辺三角形なので、
∠BFD=∠BDF=\displaystyle\frac{180-20}{2 } =80°
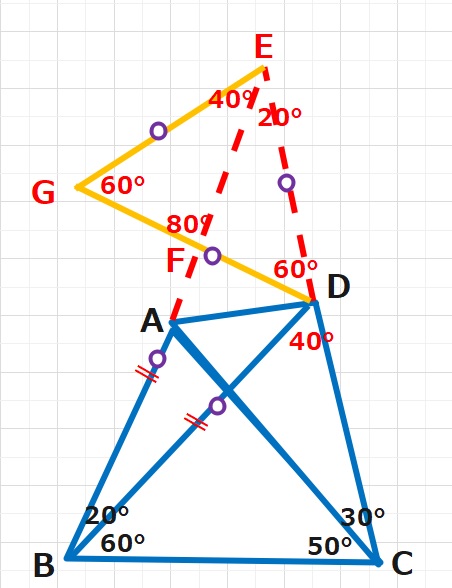
∠DBE=∠DEB=20°なので△DBEは二等辺三角形となり、DB=DE
△EFGと△DBCはEG=DBなので1辺とその間の角が等しく合同な三角形です。(図が正確でないためそのようにはみえませんが(笑))
FD=DG-FG=BF(=BD=ED)-AB(=BC)=FA となります。
よって、△FDAは二等辺三角形となり、∠FDA=\displaystyle\frac{180-80}{2 } =50°
X=∠ADB=180-(60+40+50)=30° ・・・(答え)
実はこの問題、正18角形の対角線からできています。ラングレーの問題は整角四角形の問題(4点角問題)とも言われ、10°単位のすべての4点角問題は、正18角形対角線の交点により、リスト化することができます。
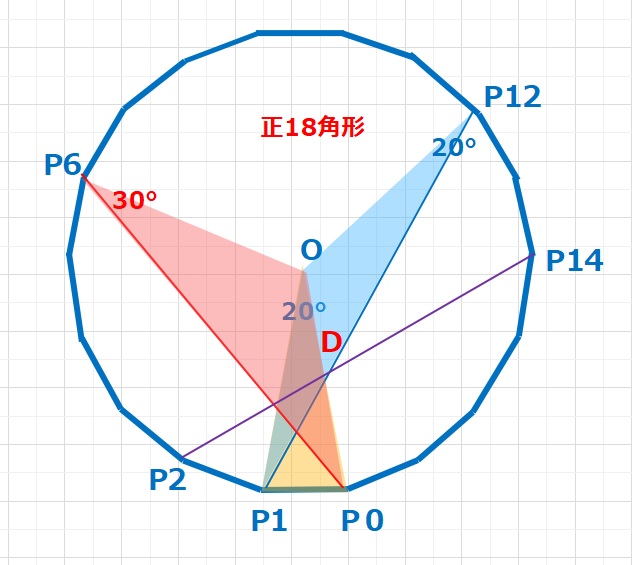
この問題は他にも色々な考え方があり、問題のシンプルさとアプローチの多さが故に注目を集めています。別解についても少しずつ掲載していきます。
コメント