算数の文章問題の定番、食塩水の問題について考えます。
時間をかけると解けるのですが、複雑な問題を5分で解くにはどうすればよいのでしょうか。
まず、食塩水の問題とはどのようなものか例題を使って考えます。
【レベル1】濃度11%の食塩水300gに含まれる食塩の量は何gですか。
%(パーセント)とはなにか? 食塩水とは?
食塩水の問題で登場するのは、 食塩と水、そしてそれを混ぜてできた食塩水。
基本的にこの3つだけです。
算数の問題で食塩水が登場するとき、理科のように「あれ食塩は全部まざるの?残らない?」
という疑問は必要ありません。基本、すべてきれいに混ざります。(笑)
さて、食塩の重さはg(グラム)で表現し、水も算数の問題ではg(グラム)で表現されます。
日常生活では水はcc(シーシー)や l(リットル)で表現しますが、水1ccの重さは1gです。
単位については別で掘り下げるとして、食塩水の問題では、
食塩も水も食塩水もgで表現されると思ってもらってよいです。
濃度とは、ある溶質が溶媒に対してどの程度溶けているかを示すものです。
今回の例では、「食塩が水に対してどの程度とけているか」ということです。
これを表すために 重量パーセント濃度という考え方を使います。
この単位が%(パーセント)となります。
%とは、「全体を100としたときにどれくらいの食塩が含まれるか」ということです。
これを押さえておけば大丈夫です。
では問題の11%の食塩水とは、食塩水100gあたりに11gの食塩が含まれているということ
を言っています。つまり 300gあたりだと11×3=33g・・(答え)ですね。
【ポイント】%は100で分けた中でどれくらい割合をしめるかを表す単位。
式では、食塩水の濃度(%)=\(\displaystyle\frac{食塩}{食塩水}\)×100と表現できます。
\(\displaystyle\frac{対象}{全体}\)で割合をだし、100を掛ける(%にする)ことで分かりやすくする、という考え方は2つのものを比較する1つの手法で、あらゆるところで活用します。
是非自分のものにしてください。
2つの濃度の異なる食塩水を混ぜてみる
【レベル2】10%の食塩水100gと8%の食塩水300gを混ぜると何%の食塩水になりますか。
食塩の問題は、食塩の量に注目しておいかけるとうまくいくことが多いです。
まず普通にといています。
10%の食塩水100gに含まれる食塩の量は10gです。
8%の食塩水300gに含まれる食塩の量は8×3=24gです。
混ぜ合わせると、10+24=34gの食塩が100+300=400gの食塩水に入っています。
よって\(\displaystyle\frac{34}{400}\)×100=\(\displaystyle\frac{34}{4}\)
=8.5%・・・(答え)となります。
この問題は簡単なのでなんとか計算できますが、複雑になってくると時間がたりません。
そこで、てんびん法(てんびん算)などが紹介されていますが、これは暗記してしまうと
将来的に意味がわからずに伸び悩んでしまいます。
今回はそのてんびん法のもととなる考え方、図形で解く方法を一緒に紹介します。
(仕組みが完璧に理解できたら、てんびん法の図でとくのは良いと思います)
下の図のように 横に食塩水の量、縦に濃度をとります。
食塩の量=濃度×食塩水の量×100となりますので、図でいうと食塩の量は
面積ということになります。
赤枠の食塩水と青枠の食塩水を混ぜ合わせると、混ぜた後の食塩水は
黄色部分で表現できます。
食塩の量はかわりませんので、差の部分
(赤+青色部分の面積)=(純粋な黄色部分の面積)となります。
ステップ1)よこの比率は100:300=1:3ですので、
面積が等しいため、たての比率は 3:1になります。
ステップ2)赤枠と青枠を混ぜ合わせた際に、縦(濃度)の差は10-8=2%です。
ステップ3)メモリ①は2%×\(\displaystyle\frac{1}{4}\)=0.5%です。
ステップ4)求める濃度(黄色)は 8+0.5=8.5%・・・(答え)
どうでしょうか。最初よりも圧倒的に計算量が少なくてすんだと思います。
面積(食塩)の関係を理解したうえで、右図のてんびんを使うと便利です。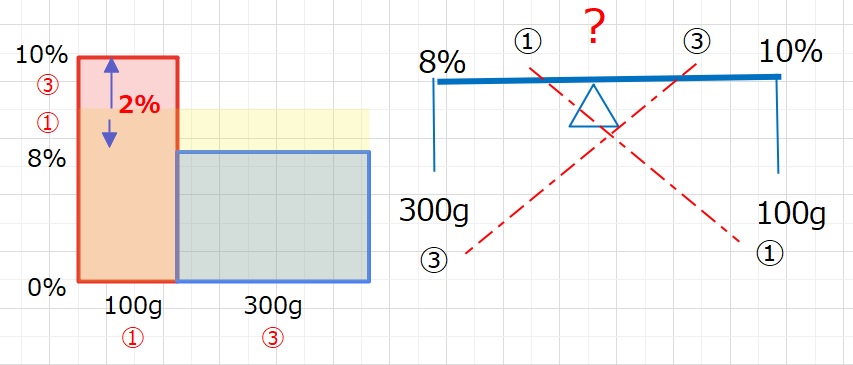
食塩は100%、水は0%の食塩水と考える
【レベル3】12%の食塩水150gに食塩を加えたら、濃度が20%になりました。
何gの食塩を加えましたか。
食塩は100%の食塩水ですので、下の図のようになります。
⑩=150g となるので、①=15g・・・(答え) です。
左図を理解して、右図をつかいましょう。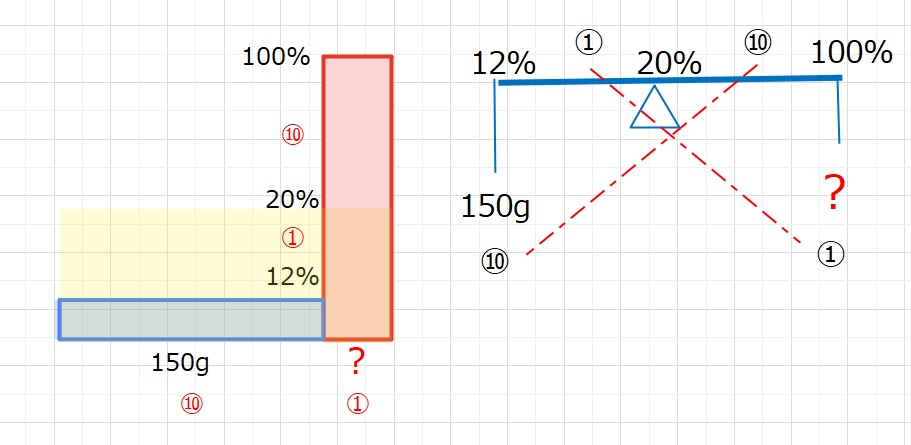
【レベル4】18%の食塩水200gに水40gを加えると、濃度は何%になりますか。
水は0%の食塩水なので、下図のようになります。
よって、18×\(\displaystyle\frac{5}{6}\)=15%・・・(答え)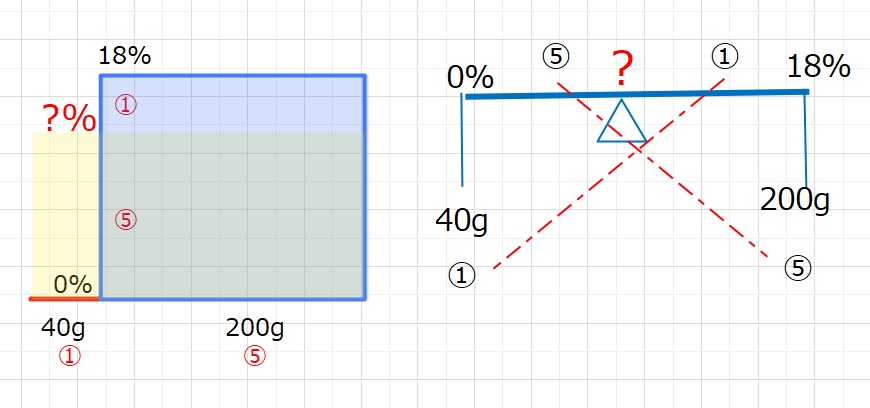
水が蒸発する問題
【レベル5】8%の食塩水250gから水を蒸発させて、10%の濃度の食塩水を作りました。
蒸発させた水は何gですか。
0%の食塩水を取り除くことになりますので、下の図のようになります。
①=250×\(\displaystyle\frac{1}{5}\)=50g・・・(答え)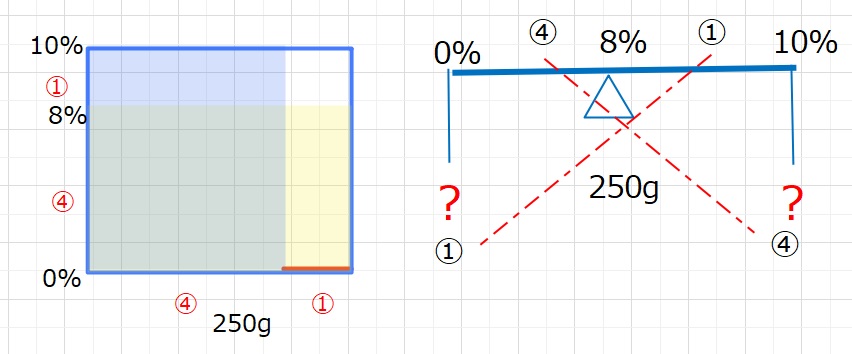
食塩水をこぼした後に水を加える
【レベル6】15%の食塩水600gをこぼし、こぼした食塩水と同じ量の水を加えたら、
濃度が8%になりました。こぼした食塩水は何gですか。
こぼした後の食塩水の食塩の量が一定なことに注目します。食塩の量は面積です。
下の図のようになるので、600×\(\displaystyle\frac{7}{15}\)=280g・・・(答え)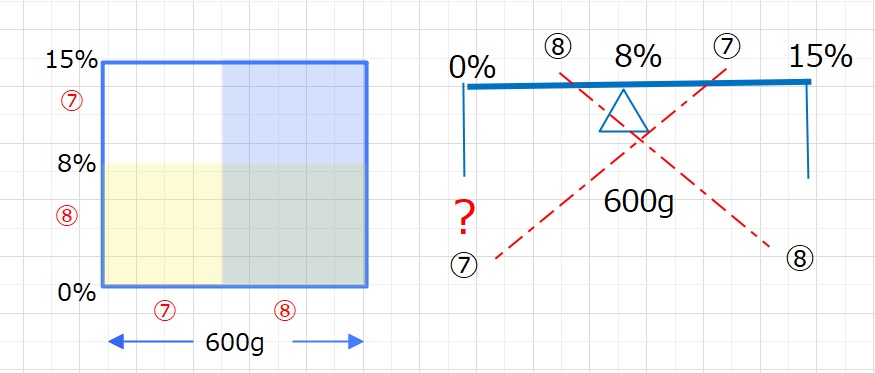
コメント