開成中学 2002年入試問題より
【問題】A、B、C3つの容器に食塩水が200gずつ入っています。
次のような操作をしました。
容器A内の食塩水100gを容器Bに移し、よくかき混ぜます。
次に、容器B内にできた食塩水100gを容器Cに移し、よくかき混ぜます。
次に、容器C内にできた食塩水100gを容器Aに移し、よくかき混ぜます。
以上の操作後の容器A内の食塩水の濃度は5%、容器B内の食塩水の濃度は、
はじめに容器A内にあった食塩水の濃度の2倍、容器C内の食塩水の濃度は、
はじめに容器B内にあった食塩水の濃度の2倍でした。
次の問いに答えなさい。
(1)はじめに容器B内にあった食塩水の濃度は、
はじめに容器A内にあった食塩水の濃度の何倍ですか。
(2)はじめに容器A、B、C内にあった食塩水の濃度はそれぞれ何%ですか。
【ヒント】整理しないと頭がこんがらがります。図を書いてひとつひとつ確実に
把握していくしかないです。文章問題の武器1,2を何度もよみ、この問題にチャレンジ
してみてください。
【解答】
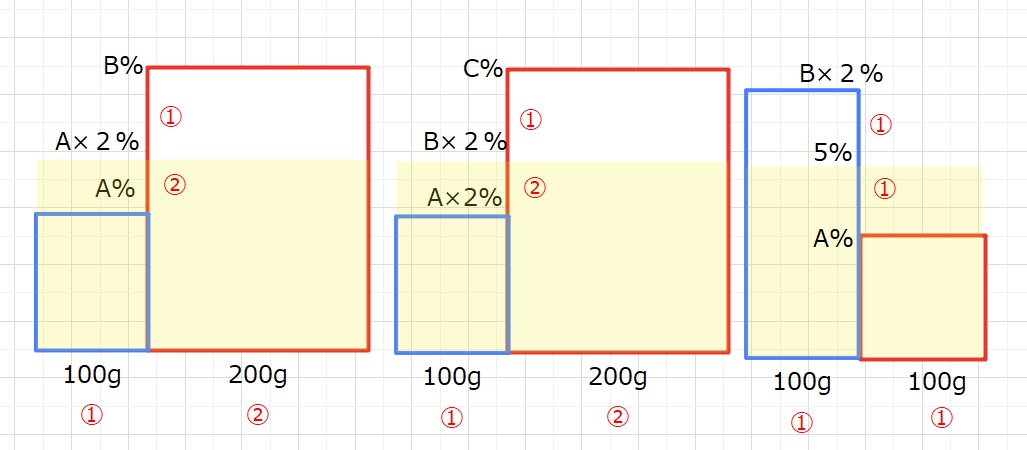
最初の食塩の濃度をAとすると、2×A-A=A が②にあたりますので、
①は \(\displaystyle\frac{1}{2}\)×Aとなります。
よってB=2A+\(\displaystyle\frac{1}{2}\)×A=\(\displaystyle\frac{5}{2}\)×A
となり、BはAの\(\displaystyle\frac{5}{2}\)倍・・・(1の答え)
さらに、下の2つ目の図(B→Cの容器へ)から B×2=\(\displaystyle\frac{5}{2}\)×A×2=5×Aより
5×A-2×A=3×A が②に相当します。よって①は\(\displaystyle\frac{3}{2}\)×A
C=2×B+①=5×A+\(\displaystyle\frac{3}{2}\)×A=\(\displaystyle\frac{13}{2}\)×Aとなります。
下の3番目の図(C→Aの容器へ)より、2×B=5×Aとなり、5%は3×Aに相当し、
A=\(\displaystyle\frac{5}{3}\)=1\(\displaystyle\frac{2}{3}\)%・・(②の答え)
B=\(\displaystyle\frac{5}{2}\)×A=\(\displaystyle\frac{5}{2}\)×\(\displaystyle\frac{5}{3}\)=\(\displaystyle\frac{25}{6}\)=4\(\displaystyle\frac{1}{6}\)%・・(2の答え)
C=\(\displaystyle\frac{13}{2}\)×A=\(\displaystyle\frac{13}{2}\)×\(\displaystyle\frac{5}{3}\)=\(\displaystyle\frac{65}{6}\)=10\(\displaystyle\frac{5}{6}\)%・・(2の答え)

コメント