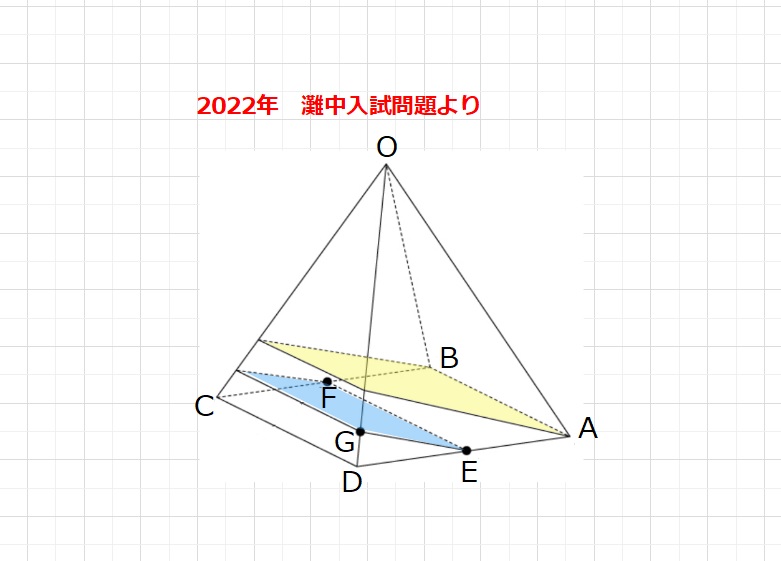
灘中学 2022年入試問題より
この問題、絶対に解いてほしい問題です。とてもよくできていると思います。
是非なんどもなんども自分のものになるまで解いてください。
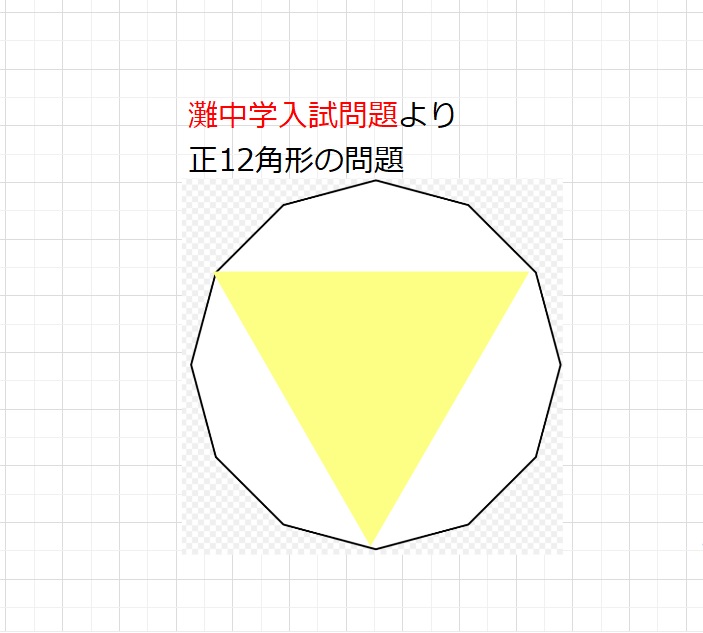
【問題】図のように1辺の長さが1cmの正12角形があります。
この正12角形の面積は、一辺の長さが1cmの正三角形12個の
面積の和よりも、ア㎠大きいです。また、下図の色のついた部分の面積は
1辺の長さが1cmの正三角形6個の面積の和よりも、
イ㎠大きいです。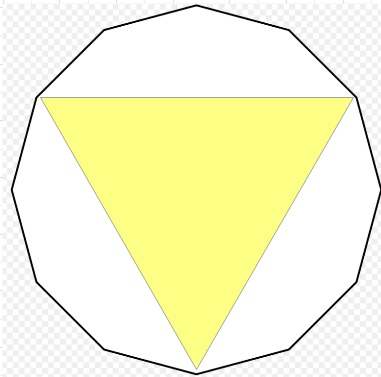
【ヒント】1辺が1cmの正三角形ということで、まず下のようにしてみました。
以前算数オリンピックで出題されたテーマとほぼ同じ問題です。
算数オリンピックで出題された問題は、下図の面積を求めるというものでした。
問題を解くにあたり、とても重要な三角形は下図の三角形です。
これは、三角定規で有名な、45°,45°,90°の直角三角形と30°,60°,90°の直角三角形
と同じくらい重要な三角形です。
一辺の長さを②としたとき、これが底辺になり、さらに高さが①になります。
よって面積は②×①×\(\displaystyle\frac{1}{2}\)=①となります。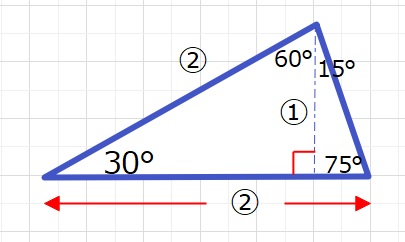
【解答】下の図のように、1辺が1cmの正三角形を12個書くと、
1辺が1cmの正方形が6個残る。
よって、6㎠・・・(アの答え)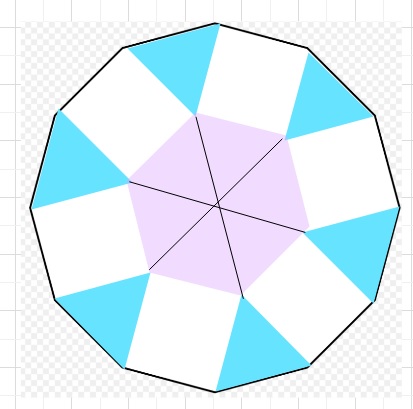
オレンジ部分は1辺1cmの正方形、ブルーは1辺1cmの正三角形となります。
よってオレンジ部分の半分(直角二等辺三角形)の面積は\(\displaystyle\frac{1}{2}\)となり、
1辺が1cmの30°の二等辺三角形の面積は\(\displaystyle\frac{1}{4}\)です。
紫の正三角形以外の部分は、1辺1cmの正三角形が6個と
直角三角形が6個、30°の二等辺三角形が3個で構成されてます。
つまり、1辺が1cmの正三角形6個+3+\(\displaystyle\frac{3}{4}\)となります。
正三角形1つの面積を①とすると、
求める面積=⑫+6-(⑥+\(\displaystyle\frac{15}{4}\))
=⑥+6-\(\displaystyle\frac{15}{4}\)=⑥+\(\displaystyle\frac{9}{4}\)
となり、正三角形6個の面積より\(\displaystyle\frac{9}{4}\)大きい・・(イの解答)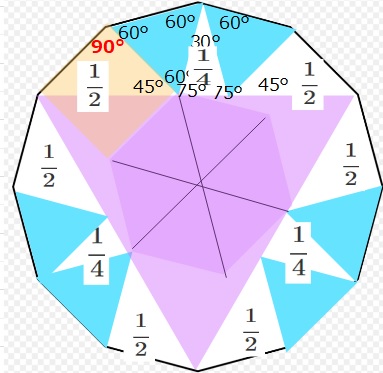
【おまけ1】せっかくですので正12角形の関連問題を2つご紹介します。
ご説明は省かせていただきます。
ジュニア算数オリンピック2019トライアル
図は、面積が72㎝2の正十二角形に、正十二角形と
1辺の長さが等しい正三角形を組み合わせた図形です。
色のついた部分の面積は何㎝2ですか。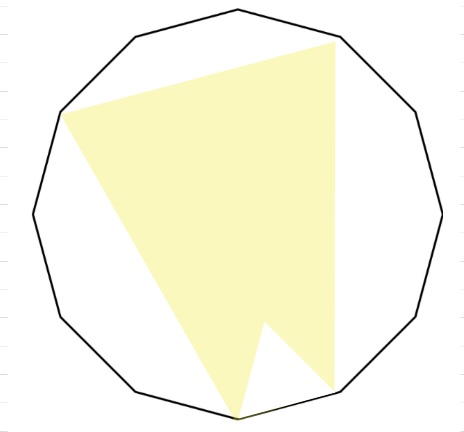
【ヒントと解答】36㎝2 ・・・(答え)
下図はヒントです。ほぼ解答ですが。(笑)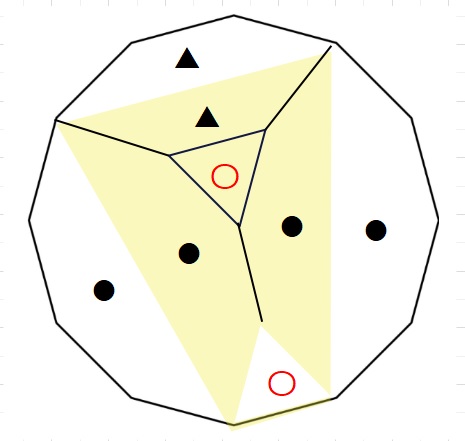
【おまけ2】赤色部分の面積が100㎠のとき、正12角形の面積はいくらですか。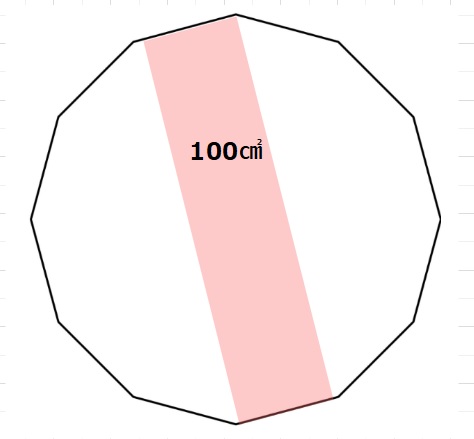
【ヒントと解答】300㎠・・・(答え)
正12角形を12等分した二等辺三角形1つの大きさ=25㎠となります。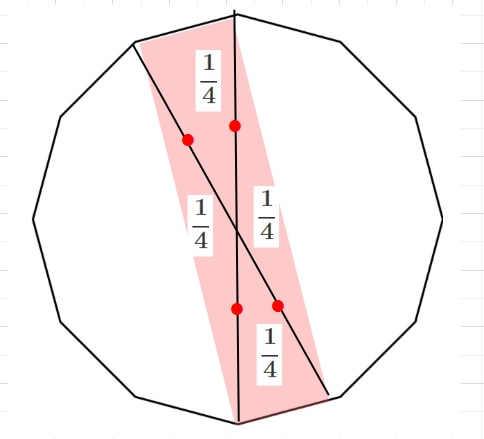
コメント