灘中学 2022年入試問題より
【問題】図のように体積が144㎤の四角すいO-ABCDがあります。
辺OA,OB,OC,ODの長さはすべて等しく底面は正方形ABCDです。
Eは辺ADの真ん中の点、Fは辺BCの真ん中の点です。
GはOD上の点で、OGの長さはGDの長さの5倍です。この四角すいを
3点E,F、Gを通る平面と、その平面に平行でAを通る平面で3つの
立体に切り分けたときOもDも含まない立体の体積はア㎤です。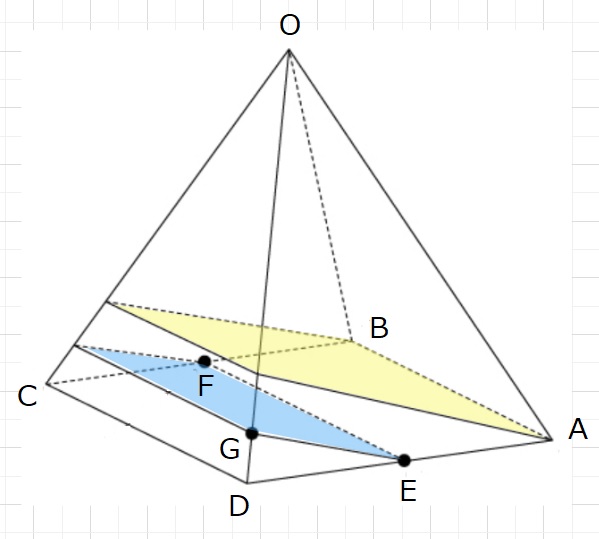
【ヒント】
図のように、H,I,J,K,L,N,N,Pをとります。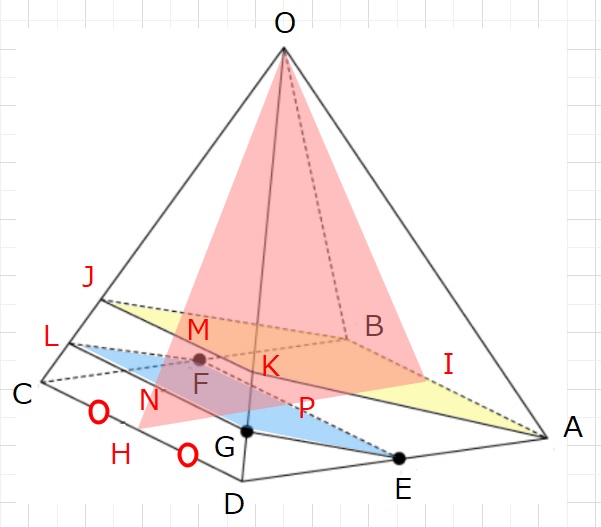
断面図△OHIを切り口として考えると、△OMI:四角形MNPI:△NHP=8:3:1です。
O-ABCDの体積は
底面OHI×高さの平均=底面OHI×(O+CD+AB)×\displaystyle\frac{1}{3}
=12×(0+6+6)×\displaystyle\frac{1}{3}=48
この体積を求める考え方を一度経験していないとこの問題は難しいかもしれません。
厳密に考えると難しいので、感覚的につかむのがよさそうです。
O-ABCDは144㎤なので、144=48×3より全体を3倍して
△OMI:四角形MNPI:△NHP=24:9:3 とわかります。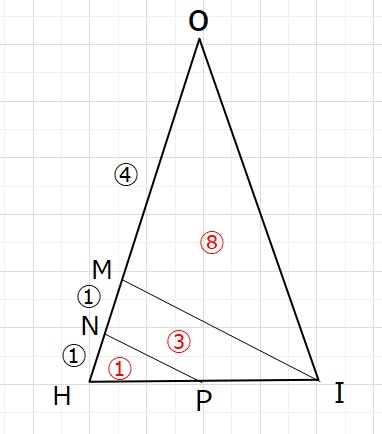
【解答】
O-JKABの体積: 三角形OMI×高さの平均=24×(O+JK+AB)×\displaystyle\frac{1}{3}
=24×(0+4+6)×\displaystyle\frac{1}{3}=80
LG-CDEFの体積:△NHP×高さの平均=△NHP×(LG+CD+EF)×\displaystyle\frac{1}{3}
=3×(5+6+6)×\displaystyle\frac{1}{3}=17
求める体積は 144-(80+17)=47㎤・・・(答え)
コメント