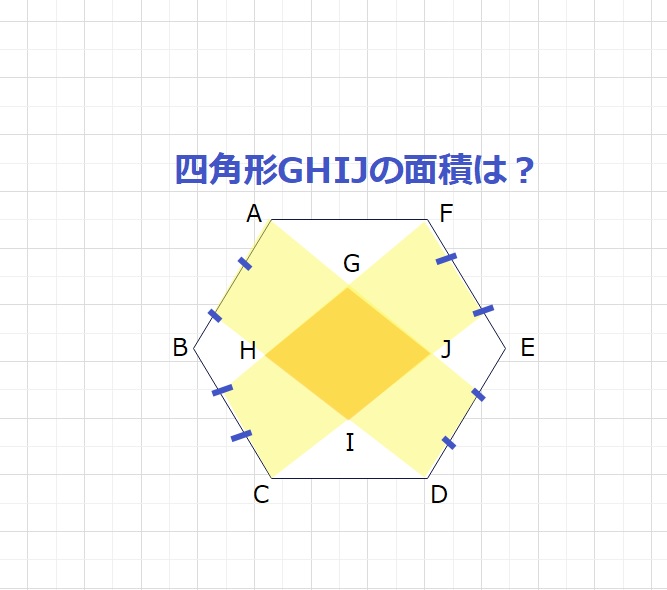
【問題】面積が36㎠の正六角形ABCDEFの角辺を3等分し、各点を結び区切った時、
四角形GHIJの面積はいくつですか。
【ヒント】
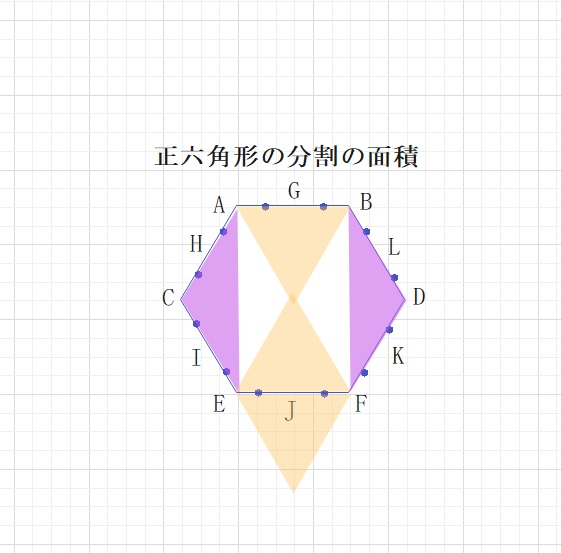
正六角形の6等分の分割方法として、前回ご紹介した下の2つをまずおさえましょう。
これを活用して解いてみます。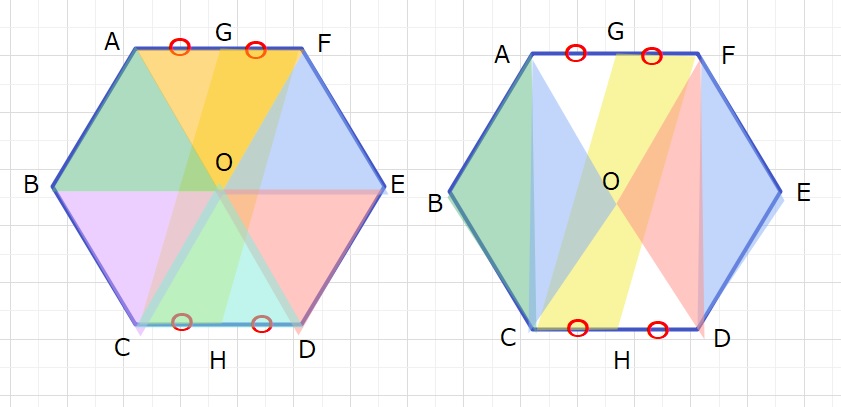
下図のブルー部分の面積は、上記の6等分をイメージすると、
△FAE=△CBD=\(\displaystyle\frac{1}{6}\)なので
ブルー部分は全体の正六角形の 1-(\(\displaystyle\frac{1}{6}\)+\(\displaystyle\frac{1}{6}\))=1-\(\displaystyle\frac{2}{6}\)=\(\displaystyle\frac{2}{3}\)
さらに四角形ANDLは AN:NB=DL:LE=2:1 なので
四角形ABDE(ブルーの面積)の\(\displaystyle\frac{2}{3}\)となります。
よって四角形ANDLは 全体の正六角形の \(\displaystyle\frac{2}{3}\)×\(\displaystyle\frac{2}{3}\)となります。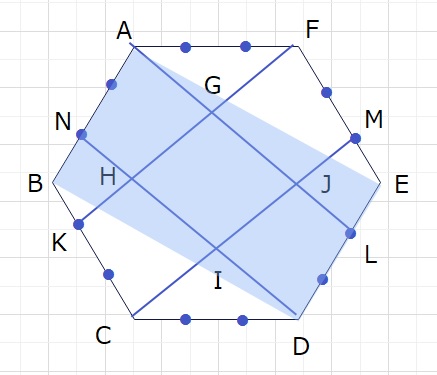
さて、ここからさらに、AG:GLは △GAF:△GKLの相似の関係を使い、
AG:GL=3:5(下の左の図)
また、AJ:JLは △MLJ:△ACJの相似の関係を使い
AJ:JL=3:1(下の右の図)
よって、AG:GJ:JL=3:3:2となります。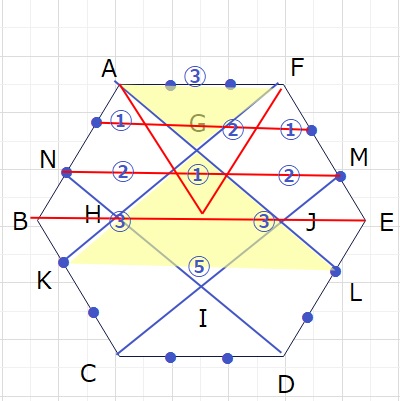
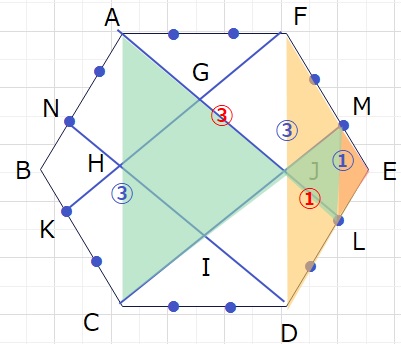
さらに下図より、 四角形GHIJは四角形ANDLの\(\displaystyle\frac{3}{8}\)です
よって求めるGHIJは 全体の正六角形の\(\displaystyle\frac{3}{8}\)×\(\displaystyle\frac{2}{3}\)×\(\displaystyle\frac{2}{3}\)となり、
正六角形の面積は36㎠なので
36×\(\displaystyle\frac{3}{8}\)×\(\displaystyle\frac{2}{3}\)×\(\displaystyle\frac{2}{3}\)=6㎠・・・(答え)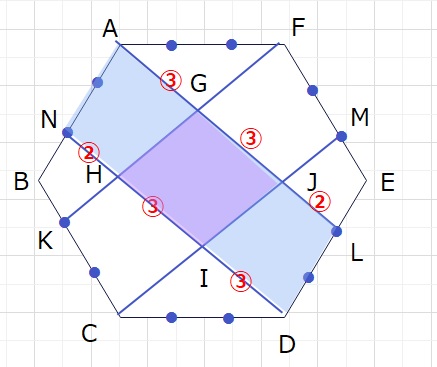

コメント