2017年 筑波大学付属駒場中学入試問題より
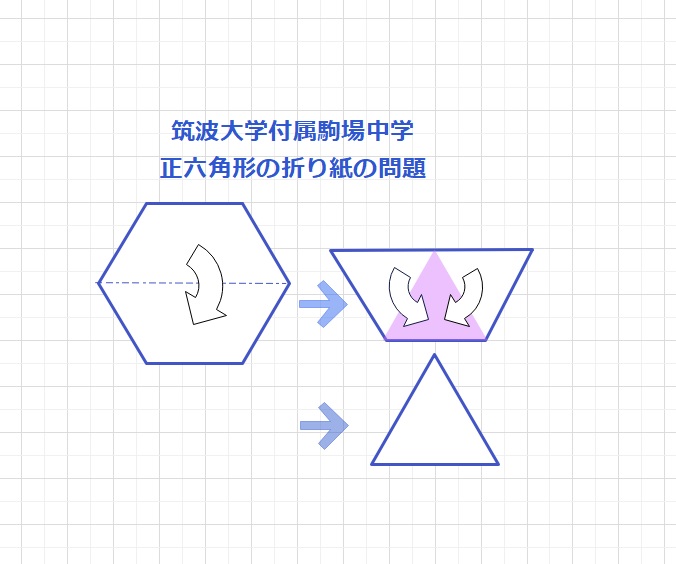
【問題】正六角形の紙に次のような操作を行います。
操作1)図の正六角形を点線で半分におり、
さらにできた台形を点線で、両側の正三角形を真ん中に折り重ね、
図のような正三角形にする。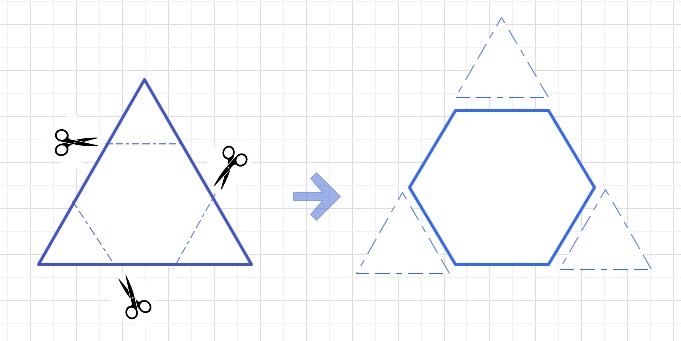
操作2)操作1でできた正三角形を図のようにハサミで切り、
正六角形を残す。
上の操作1→操作2を1回とかぞえ、操作の後に残った正六角形に対して、
続けて操作を行っていきます。
初めの正六角形の紙は、面積が81㎠です。
(1)1回目の操作の後に残った正六角形の紙を、全部ひろげます。
同様な形の紙になりますか。下図の点線をはじめの正六角形として、
広げた紙の形を書きなさい。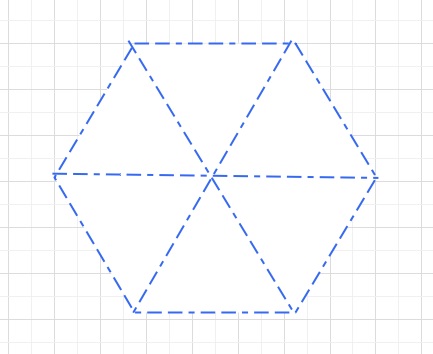
(2)2回目の操作の後にのこった正六角形の紙を、全部ひろげます。
広げた紙の面積を求めなさい。
(3)3回目の操作の後にのこった正六角形の紙を、全部ひろげます。
広げた紙にはいくつか穴があいています。
面積が最も大きい穴は、何㎠ですか。
【ヒント1】
1回目の操作を行った紙を途中までひろげると、下のようになります。
黒の部分はハサミで切り落とした部分です。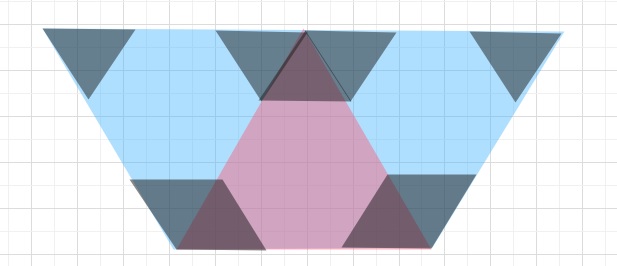
【ヒント2】最初の正六角形は、黒い小さな正三角形を1つの単位として
できていることがわかります。最初の正六角形は、黒い正三角形が9×6=54個分となります。
また1回目の操作の後にできた正六角形は黒い正三角形6個分となります。
【ヒント3】
1回目の操作でできる正三角形は 54個で1つの面積は
81×\displaystyle\frac{1}{54}= \displaystyle\frac{3}{2}㎠
正六角形 1つの面積は\displaystyle\frac{3}{2}×6=9㎠
2回目の操作後にできる正六角形は 9×\displaystyle\frac{1}{9}=1㎠
3回目の操作後にできる正六角形は 1×\displaystyle\frac{1}{9}=\displaystyle\frac{1}{9}㎠となります。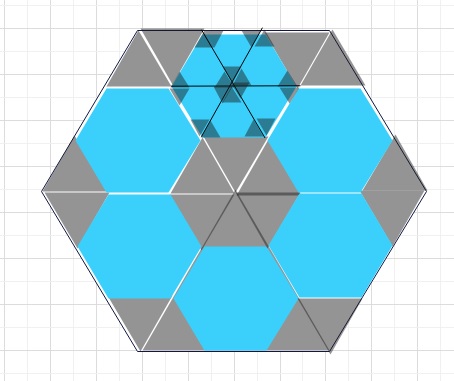
【解答】
(1)の解答は下図のとおり。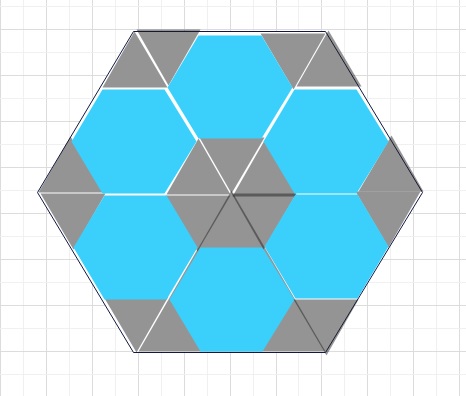
(2)最初の正六角形は黒い正三角形 9×6=54個
ブルーの正六角形 は黒い正三角形6個分なので、ブルーの部分の合計は
6×6=36個分
操作1回行うことにより、最初の正六角形の\displaystyle\frac{6×6}{9×6}=\displaystyle\frac{6×6}{9×6}=\displaystyle\frac{2}{3}倍となるので、
操作1回目の終了後の面積は、
81×\displaystyle\frac{2}{3}となり、小さい正六角形1つの面積は
81×\displaystyle\frac{2}{3}×\displaystyle\frac{1}{6}=9㎠となります。
操作2回目の終了後はさらに、9×\displaystyle\frac{2}{3}=6となり、
この正六角形が6個あるので、6×6=36㎠・・(答え)
(3)1回目の操作後にできる一番大きな穴は正六角形1つで9㎠となります。
2回目の操作後にできる追加の穴は、正六角形の1つの角に正三角形が4個追加されるので、
4×6=24個分のあなで、これは正六角形に換算すると24÷6=4個分となります。
2回目の操作後にできる正六角形の面積は1㎠なので 1×4=4㎠となります。
3回目の操作後にできる追加の穴は、正六角形1つの角に正三角形が16個追加されるので、
16×6=96個分の穴で、これは正六角形に換算すると96÷6=16個分となります。
3回目の操作後にできる正六角形の面積は\displaystyle\frac{1}{9}㎠なので
\displaystyle\frac{1}{9}×16=\displaystyle\frac{16}{9}㎠
よって求める面積は9+4+\displaystyle\frac{16}{9}
=14\displaystyle\frac{7}{9}㎠・・・(答え)
コメント