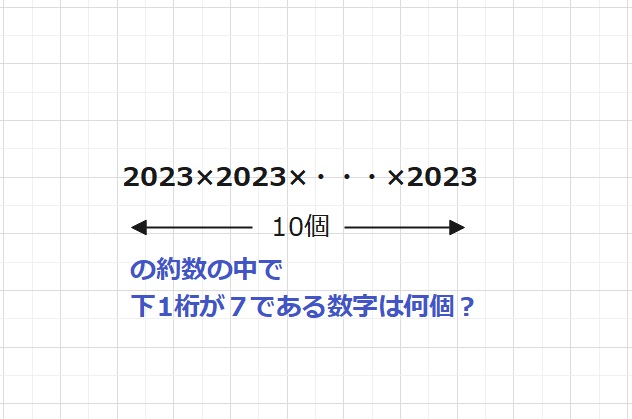
【問題】2023を10回かけた数字、2023×2023×・・・×2023の約数の中で、
下1桁が7となる数字は何個ありますか。
【ヒント】
2023=7×17×17 となります。
2023の約数は 1,7,17,7×17,17×17,7×17×17の6個となります。
すべて下1桁が7のかけ算で構成されています。
7を何度もかけていくと、下1桁は
7,9(49),3(343),1(2401)となり、1が現れたので次は1×7で最初の数字にもどります。
つまり 7,9,3,1,7,9,3,1・・と 下1桁は7,9,3,1を繰り返します。
【解答】縦に7を掛けた回数、横に17を掛けた回数をかきます。
7,17を0回かけた数字はどちらも1とします。
2023を10回かけた数字は 7を10回、17を20回かけた数字と
なります。
下1桁は7となるのは 7と17を合わせて1回、5回、9回、13回、17回・・
掛けた時となります。
下の表より
1回 2個
5回 6個
9回 10個
13回 11個
17回 11個
21回 10個
25回 6個
29回 2個 となります。
よって (2+6+10+11)×2=58個・・(答え)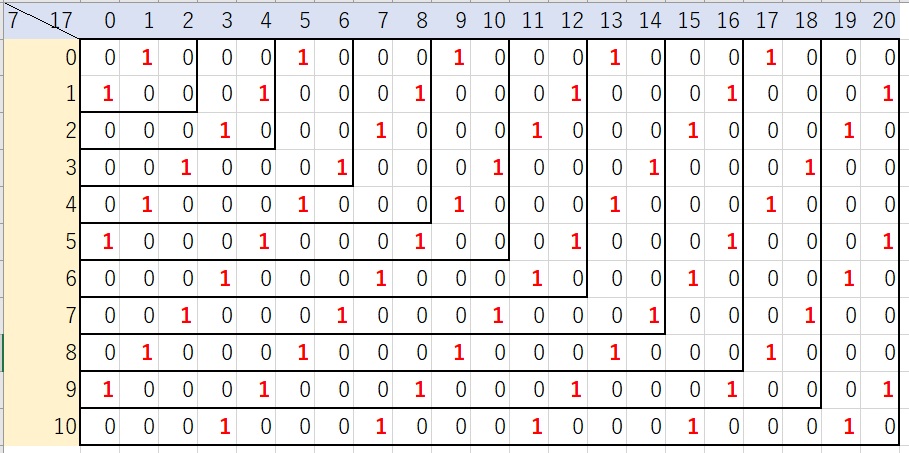


コメント