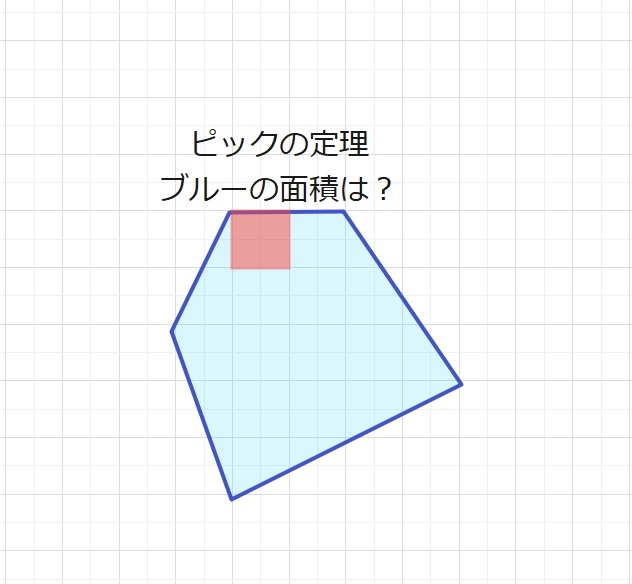
【例題】赤い正方形の面積が1㎠のとき、青の5角形の面積はいくつですか。
今回は、ピックの法則といわれているものをご紹介します。
格子点を線で結んでできる図形を格子多角形といいます。
格子多角形は普通に面積を求めることができますが、下のような式でも計算できます。
(面積)=(まわりの点の数)×\(\displaystyle\frac{1}{2}\)+(内部の点の数)ー1
この式は算数の範囲での証明は難しいですが、イメージだけ共有します。
下の左図のようなハートマークを格子上に書いたとします。この格子単位を少し
大きくすると右図のようになります。これはカメラの画素やプリンタの解像度と
同じような絵の作り方をイメージするとよいと思います。
なかなかお伝えしたいイメージの図が書けませんでしたので、
解像度とは? 図解で超わかりやすく解説【 PPI / DPI 】 | 321web さんの図を
お使いさせていただきました。あくまでもイメージです。
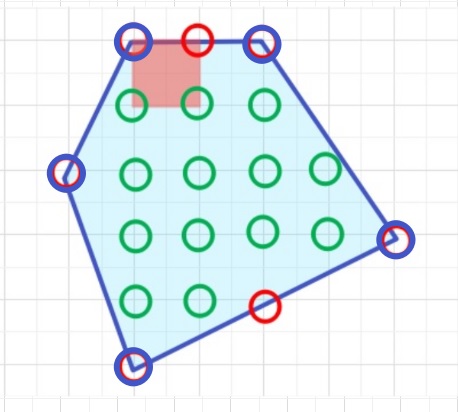
今回の例の図で考えていきます。今、格子単位を赤の正方形としたときに、
1つの格子単位の4角の面積への影響度をイメージしてみます。
格子単位4角の緑の角の部分は100%中に入っているので影響度100%(1)となります。
格子単位4角の赤い角の部分は線上にあり、50%(\(\displaystyle\frac{1}{2}\))の影響度となります。
ここまではイメージしやすいと思いますが、青い角の部分は少し難しいです。
点(円)のうちに入っている角度分影響していると考えると、青い角の内側の角度の合計は
多角形の内角の和にあたります。
N角形の内角の和は、180×(N-2 )=(180×N-360)度ですので
これを全体の360°でわると
\(\displaystyle\frac{180×N-360}{360}\)=\(\displaystyle\frac{1}{2}\)×N-1
となります。
青と緑と赤の点の合計を求めると
\(\displaystyle\frac{1}{2}\)×(青い点)-1+\(\displaystyle\frac{1}{2}\)×(赤い点)+緑の点
=(青と赤の点)×\(\displaystyle\frac{1}{2}\)+(緑の点)-1
となります。
実際に計算すると、
面積=7×\(\displaystyle\frac{1}{2}\)+13-1
=3.5+12=15.5㎠ となります。
【応用】下記は2006年の女子学院中学の入試問題です。
面積が1㎠の正三角形をすきまなく敷き詰めました。3つの点A,B,Cを結んでできる
三角形の面積は何㎠ですか。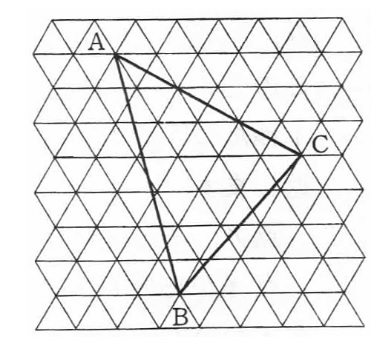
この問題は正方形ではなく正三角形×2の平行四辺形(2㎠)を1つの単位として
ピックの定理を使ってみます。
面積=5×\(\displaystyle\frac{1}{2}\)+12-1=2.5+11=13.5
平行四辺形の1つの面積は2㎠なので 13.5×2=27㎠・・(答え)
となります。ピックの定理を使うと一瞬ですね。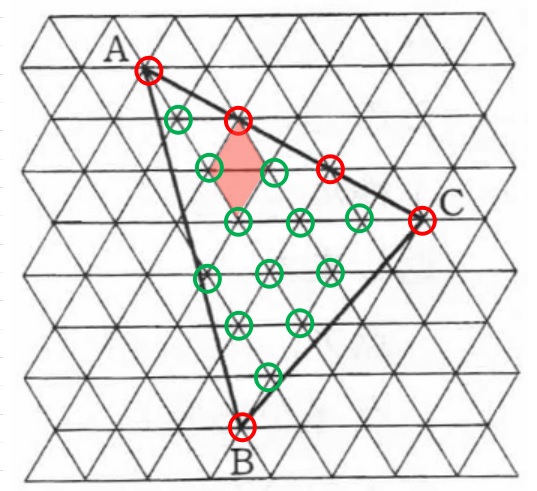

コメント