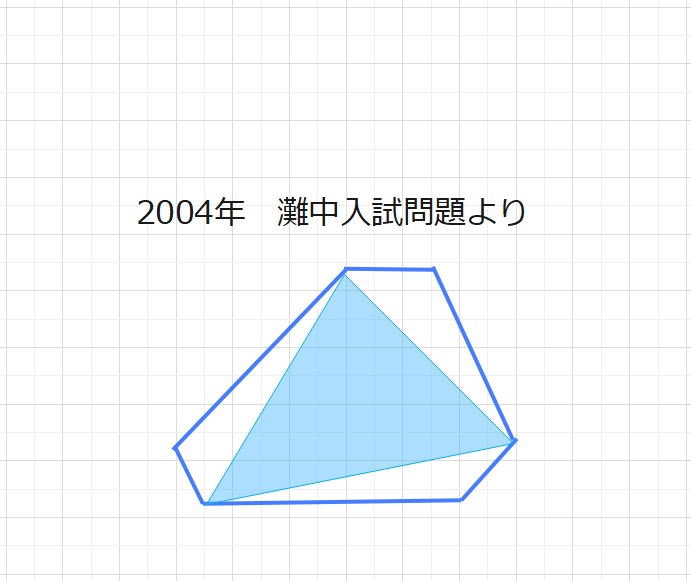
2004年 灘中学入試問題より
【問題】図の六角形の向かい合った辺は3組ともに平行で、3組それぞれについて
短い辺と長い辺の長さの比が1:3となっています。
色のついた部分の面積は、六角形の面積の何倍か答えなさい。
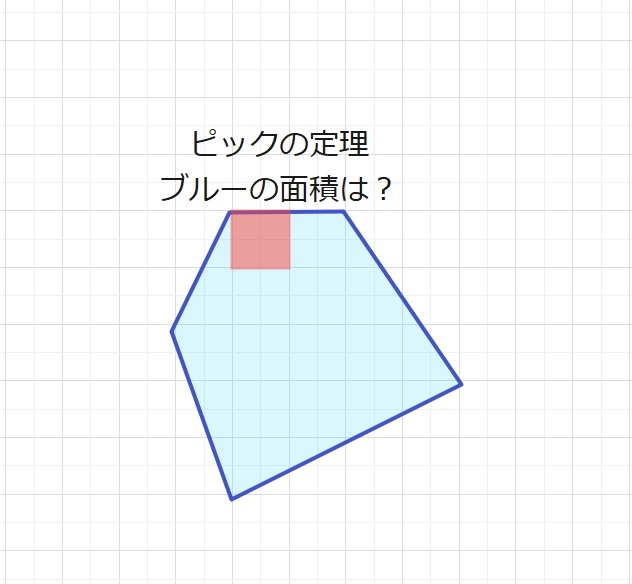
【ヒント】図形問題の武器でご紹介したピックの定理を使ってみます。
詳しくは、ゼロから始める 図形問題の武器8 ピックの定理 (格子多角形の面積) | 算数コロシアム (mathcolo.com) をご参照ください。
(面積)=(まわりの点の数)×\(\displaystyle\frac{1}{2}\)+(内部の点の数)ー1
オレンジの平行四辺形を1単位として、計算すると、
ブルーの三角形=3×\(\displaystyle\frac{1}{2}\)+6-1=6.5となります。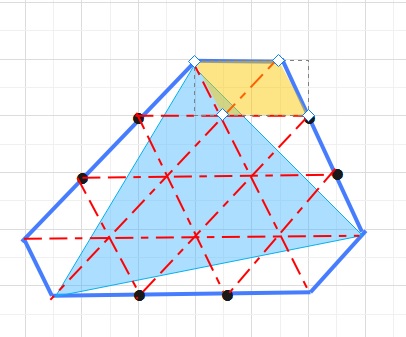
【解答】六角形は平行四辺形11個分で、ブルーの三角形の面積は6.5個分となります。
よって、六角形:三角形=11:6.5=22:13
つまり \(\displaystyle\frac{13}{22}\)倍・・(答え)
【おまけ】普通に解くと下記のような感じでしょうか。
黄色系と紫系と緑系の平行四辺形はそれぞれ三角形6個分です。
薄い図形と濃い図形はそれぞれ同じ面積となっています。
六角形は三角形22個分となっています。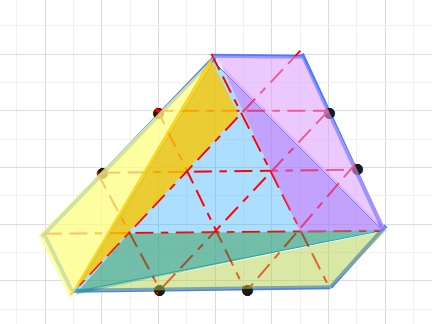
コメント