難易度
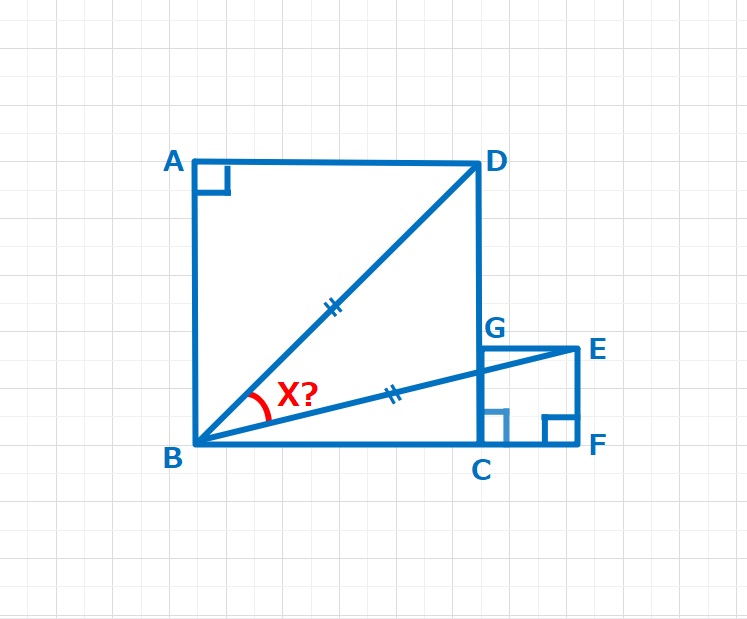
正方形ABCDの対角線をBDとします。BD=BEとなるように正方形GCFEをツクルト、X=∠DBEは何度ですか。
【ヒント】
BF=DHとなるように△BFEを移動した三角形が△DHGです。
よって△DBGはDB=DGの二等辺三角形となりますが、よくみると、、、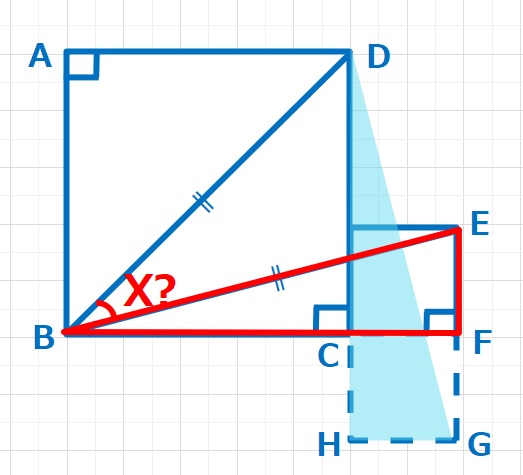
BE=BGでもあるので、下図のように△DBGは正三角形となります。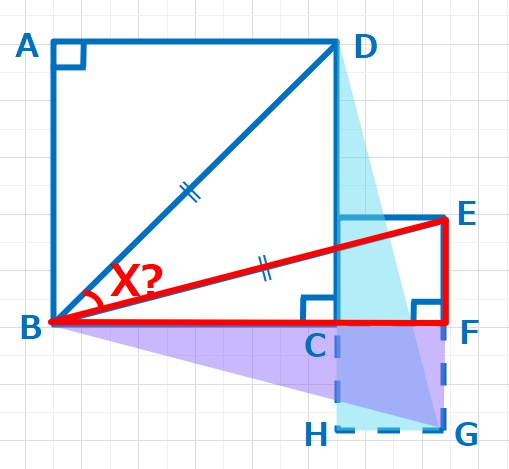
【解答】
BF=DHとなるように△BFEを移動し、点H,Gをつくると
△DBGは正三角形となります。∠BDG=60°、∠BDC=45°なので∠GDH=15°=EBF
よってX=45-15=30°・・・(答え)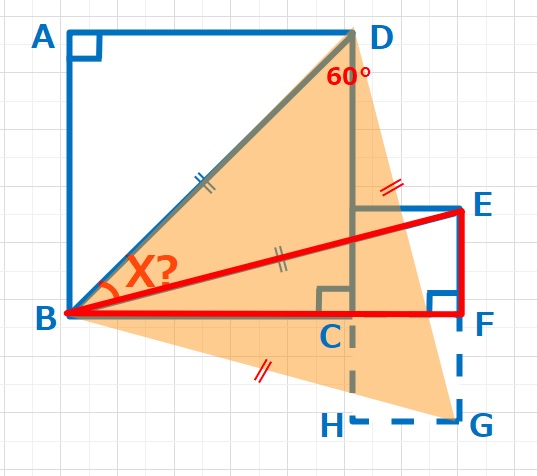
おまけ
じつはこれを活用して、中学でならう三平方(ピタゴラス)の定理が証明できます。
一辺がa の正方形と一辺がbの正方形の面積の合計は(a×a)+(b×b)ですが、これを右のように変形すると、一辺がcの正方形の面積 c×cと同じになります。よって a×a + b×b = c×c が導かれます。これは中学校で習いますが、小学生でも使うと便利な時がありますので、知ってると得かもですね。理解できる人は覚えておきましょう。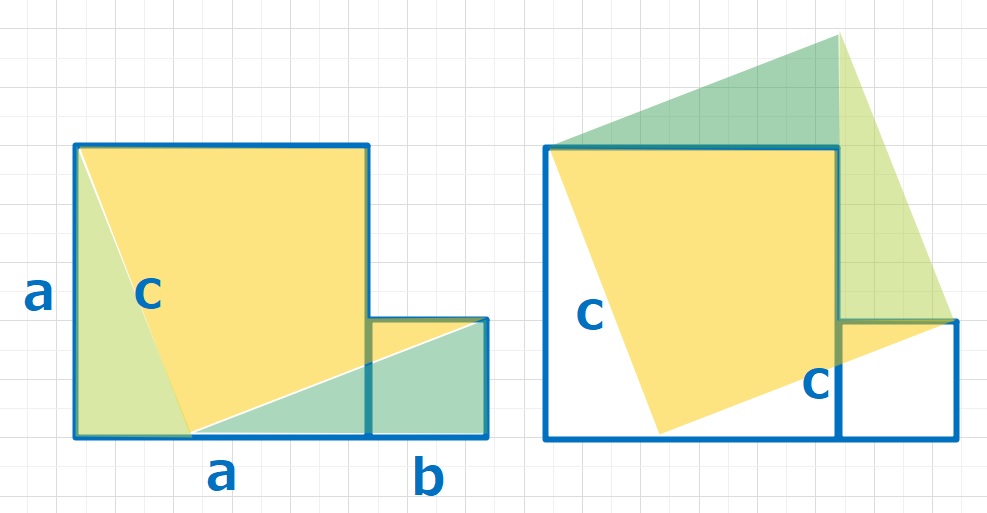
コメント