【例題】
今回は、ある図形を特定の軸を中心に回転してできた回転体の体積について考えます。
これも前回の図形の武器9でご紹介した金太郎あめの的な考え方で理解できると思います。
今、下のような平行四辺形があるとします。この平行四辺形を軸を中心に回転してできる回転体の体積はどうなるでしょうか。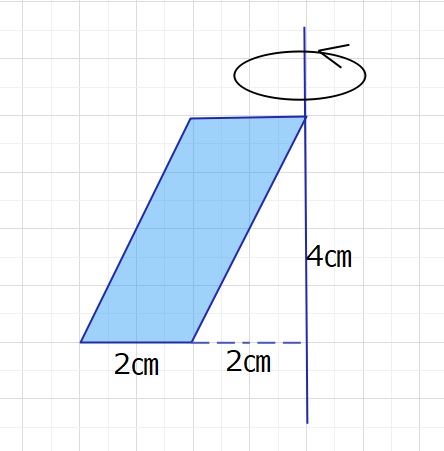
平行四辺形の面積は2×4=8となります。
通常の解き方ですと、赤い三角形を回転した円すいからオレンジと緑の回転した円すいをひいて青い回転体の体積を求めることになります。因みにオレンジと緑の円すいの体積は等しくなります。
4×4×3.14×8×\(\displaystyle\frac{1}{3}\)‐ 2×2×3.14×4×\(\displaystyle\frac{1}{3}\)×2=32×3.14=100.48㎠となります。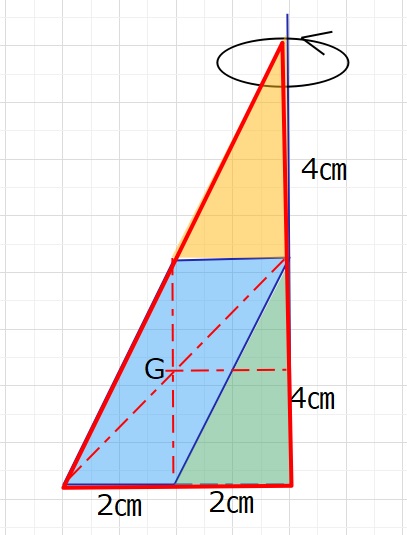
【裏ワザ】パップス・ギュルダンの定理
(回転体の体積)=(断面積)×(断面積の重心の移動距離)
断面積とは今回は青の平行四辺形=2×4=8となります。
断面積の重心とはどこでしょうか。
今回の平行四辺形の場合、重心は対角線の交点Gということがわかっています。
じつは、この重心がわからない場合が多く、普通に解いた方が早い場合が多いです。
今回はGがわかっていますので、Gの移動距離は 半径2㎝の円周、つまり
2×2×3.14=4×3.14となります。
よって回転体の体積は 8×4×3.14=32×3.14=100.48となります。
【おまけ】1月16日更新
1月14日の灘中入試問題で見事出題されました。今後のために追加更新いたします。
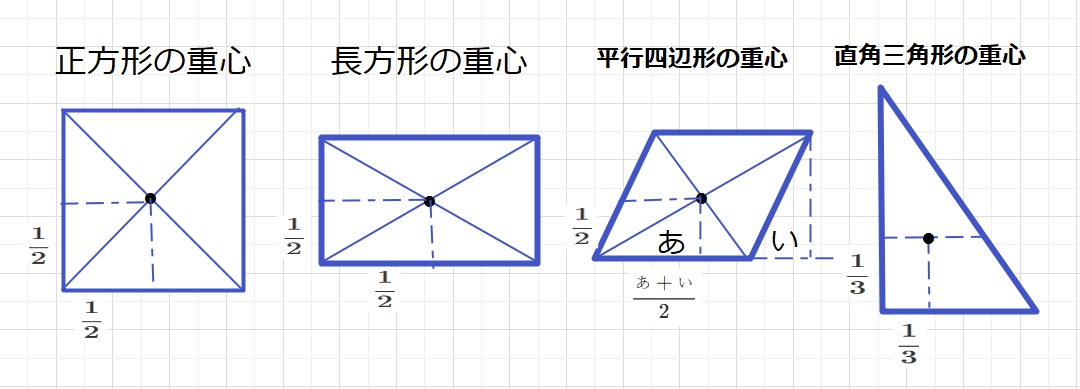
代表的な図形の重心について、下記のことがわかっていれば、さらに時間短縮になります。
垂直な縦の棒を中心に図形を回転するとき、パップス・ギュルダンの定理で重要なのは、
それに垂直な横の長さとなります。


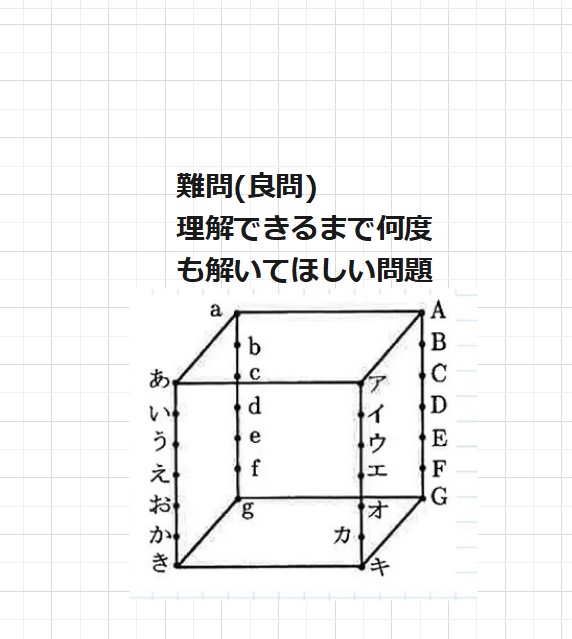
コメント