今日はベンツ切りといわれる方法について書きます。
今下のような三角形ABCがあるとき、BD:DC=ア:イがわかっているとします。
この時、△BOA:△COA=ア:イがなり立つというものです。
シンプルですが、これを応用することで、様々な問題が解けますので
とても重要です。どうしてそうなるのか、理屈をしっかり押さえておきたいです。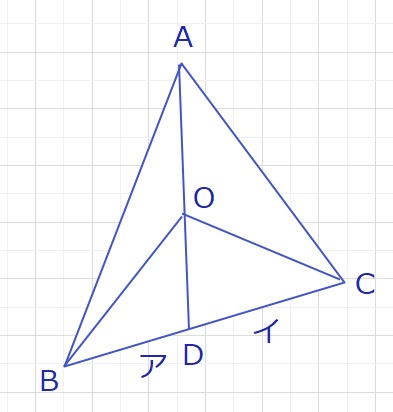
まず、△OBD:△OCDに注目すると、BC,CDをそれぞれ底辺と考えたとき、
高さは、OHで共通です。
よって、△OBD:△OCD=BD:CD=ア:イが成り立ちます。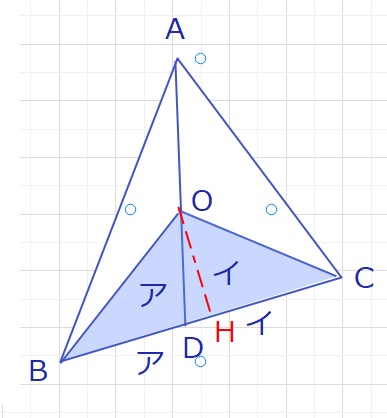
△OBDと△OCDにおいて、ODを底辺と考えると、高さはそれぞれBJ,CIとなり、
BJ:CI=ア:イとなります。
次に、△BAO:△CAOはAOを底辺とすると、高さはそれぞれBJ,CIとなり、
△BAO:△CAO=ア:イが成り立ちます。
つまり、BD:DC=ア:イのとき△BAO:△CAO=ア:イが成り立ち、
また逆に、△BAO:△CAO=ア:イのとき、BD:DC=ア:イが成り立ちます。
これを使うことによって、のちに習うチェバの定理・メラネウスの定理という
ものも証明することができます。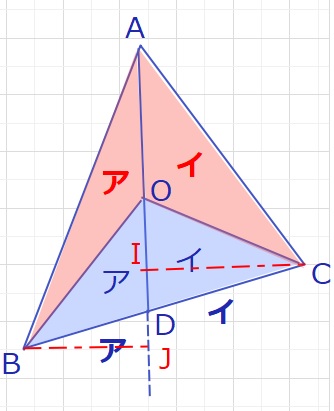


コメント