2021年 大宮開成中学入試問題
2010年 駒場東邦中学入試問題 改題より
【問題】
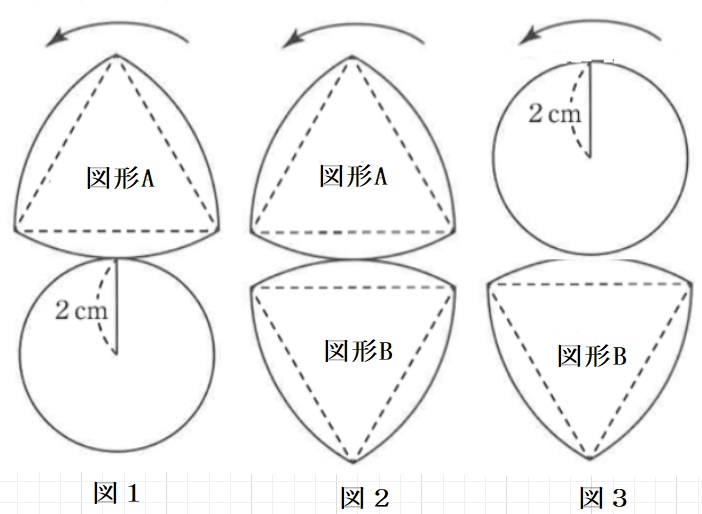
下図のように半径4㎝、中心角60°のおうぎ形を3つ組み合わせた図形Aがあります。
この図形はルーローの三角形とよばれ、自動掃除機ロボットなどの図形のデザインにも
図形の性質が活かされています。次の問いに答えなさい。
ただし円周率は3.14とします。
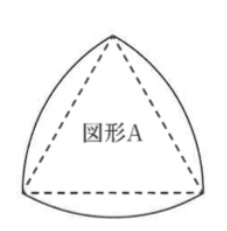
(1)図1のように図形Aと半径2㎝の円があり、図形Aが円のまわりを
すべることなく転がります。図形Aが通過する部分の面積は何㎠ですか。
(2)図2のように図形Aと同じ図形Bがあり、図形Bが固定されています。
図形Aが図形Bの周りをすべることなく転がります。図形Aが通過する部分
の面積は何㎠ですか。
(3)図3のように図形Aと同じ図形Bがあり、図形Bが固定されています。
半径2㎝の円が図形Bの周りをすべることなく転がります。円が通過する
部分の面積は何㎠ですか。。
【ヒント】
問題にも書いているとおり、P社のお掃除ロボットの名前も同じようなネーミングでした(笑)
その他にも某社のロータリーエンジンに利用されたりと私たちの生活の色々なところで
利用されています。
ルーローの三角形のポイントは定幅図形(ていふくずけい)であるということです。
具体的には、ルーローの三角形を転がすと、高さが一定の幅のまま転がります。
(1)
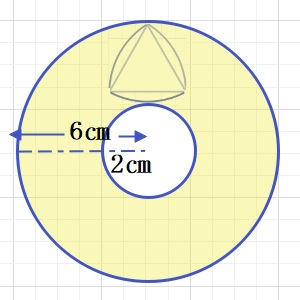
(2)少しわかりにくいですが、イメージだけ図にしました。(正確にかけてません)
①半径8㎝の外側の円と半径4㎝の内側の円に挟まれた面積ゾーン。
②半径が4㎝のおうぎ形ゾーン。
の2つの図形が60°の間隔で3つずつあります。実は(3)と同じ問題です。
(3)で簡単に説明します。
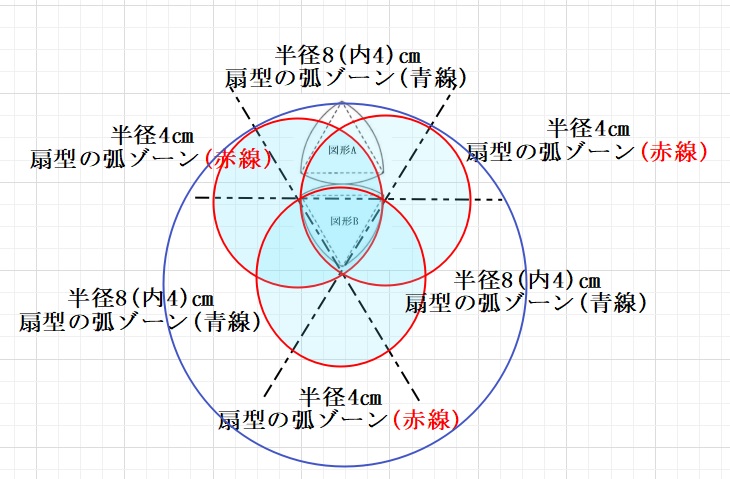
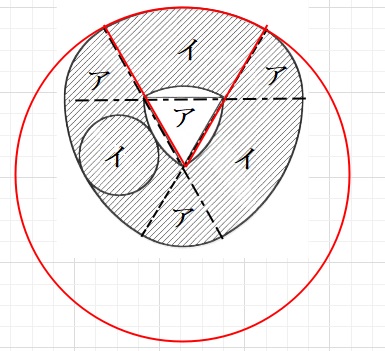
(3)半径4㎝ののおうぎ型(ア)のゾーンと
半径8㎝の外側の円と半径4㎝の内側の円に挟まれた(イ)のゾーン。
アとイを組み合わせると、半径8㎝の60°のおうぎ型となります。
これが3個あります。
【解答】
(1)6×6×3.14-2×2×3.14=(36-4)×3.14=100.48㎠・・・(答え)
(2)正直に丁寧に計算してみます。(3)のように計算すると楽です。(笑)
(8×8×3.14-4×4×3.14)×\(\displaystyle\frac{60}{360}\)×3=48×\(\displaystyle\frac{1}{2}\)×3.14=24×3.14
4×4×3.14×\(\displaystyle\frac{60}{360}\)×3=16×\(\displaystyle\frac{1}{2}\)×3.14=8×3.14
24×3.14+8×3.14=32×3.14=100.48・・(答え)
(3)8×8×3.14×\(\displaystyle\frac{60}{360}\)×3=32×3.14=100.48㎠・・・(答え)
コメント