※この問題は算数の範囲外の知識が一部入ってますが、先日の問題の関連として、
書きます。
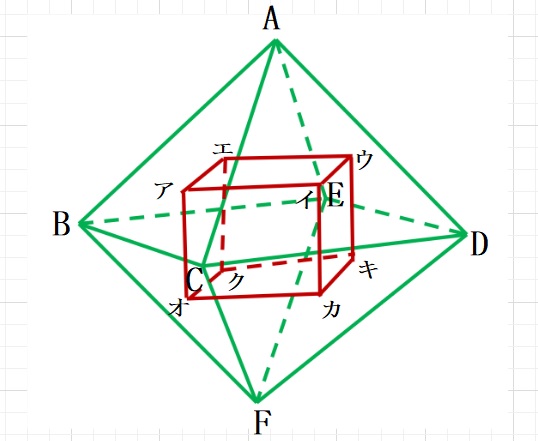
【問題】一辺が2㎝の正八面体ABCDEF(立体あ)があります。
それぞれの面(一辺が2㎝の正三角形)の重心を結んでできた立体
アイウエーオカキク(立体い)は正六面体(立方体)になることがわかっています。
(立体あ)と(立体い)の体積比はいくつですか。
重心とは三角形ABCにおいて各頂点からその対の辺の中点(真ん中の点)
を結んだ交点、つまりBC、AC、ABの中点をM,N,Lとすると
AMとBN,CLの交点のことをいいます。
【ヒント】少し、算数の範囲を超えるところがありますが、できる限りわかるように
説明します。
四面体A-BCDEの高さをAHとします。
BCの中点をMとして三角形AMHについて考えます。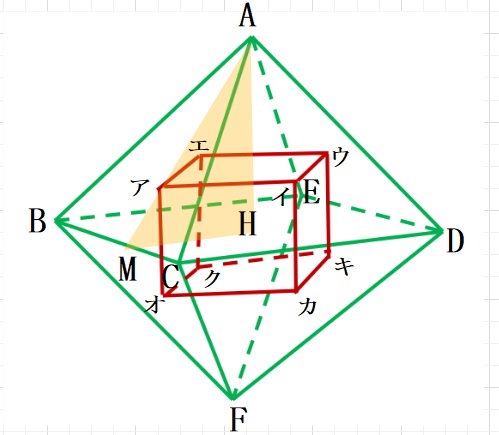
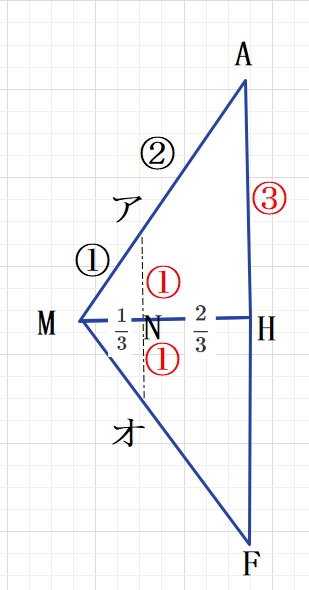
図のようにNをとると、MH=1㎝なので、MN= \(\displaystyle\frac{1}{3}\) ㎝ NH= \(\displaystyle\frac{2}{3}\)㎝となります。
【解答】正八面体の体積は2×2×\(\displaystyle\frac{1}{3}\)×AH×2=\(\displaystyle\frac{8}{3}\)×AH
正六面体の体積は \(\displaystyle\frac{2}{3}\)×AH×\(\displaystyle\frac{2}{3}\)×AH×\(\displaystyle\frac{2}{3}\)×AH=\(\displaystyle\frac{8}{27}\)×AH×AH×AH
\(\displaystyle\frac{8}{3}\)×AH : \(\displaystyle\frac{8}{27}\)×AH×AH×AH
( 立体あ):(立体い)=9 : AH×AH となります。
いま三角形AMHは直角三角形で、AH×AHはAM×AMからMN×MNを引いた数字
とわかってますので、MN=1なので AM×AM-1となります。
また三角形AMCも直角三角形で、AM×AMはAC×ACからMC×MCを引いた数字なので
AC=2、MC=1より AH×AH=2×2-1×1-1×1=2となります。
よって( 立体あ):(立体い)=9 : 2・・・(答え)
先日のお話しも参考いただけるとうれしいです。★★★☆☆中級コース 正多面体の中に正多面体 | 算数コロシアム (mathcolo.com)
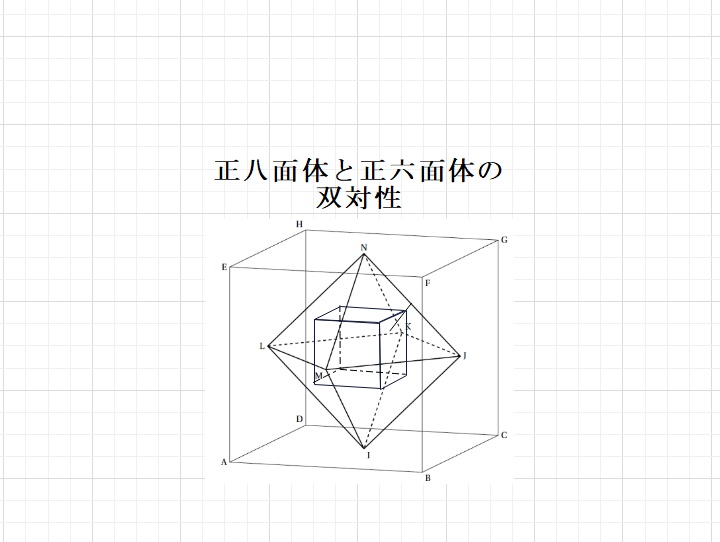
【おまけ】最初の図にもどりますと、一番大きな立法体の中の正八面体は\(\displaystyle\frac{1}{6}\)
の大きさ。さらにその中の立方体は\(\displaystyle\frac{2}{9}\)の大きさになってますので
小さな立方体は 外の大きな立方体の体積の\(\displaystyle\frac{2}{9}\)×\(\displaystyle\frac{1}{6}\)=\(\displaystyle\frac{1}{27}\)
つまり1辺の長さが大きな立方体の\(\displaystyle\frac{1}{3}\)の立方体が中に入ることになるのですね。これを確認したかっただけの問題でした。(笑)
コメント