★★☆☆☆初級コース　知っておきたい三角すい

2.0

【問題】
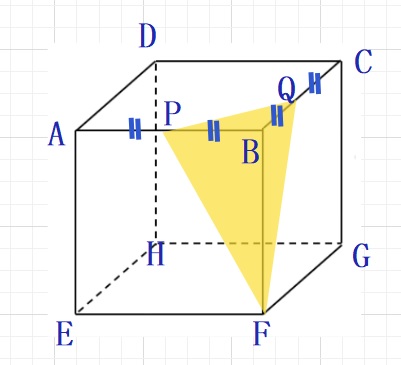
　図のように1辺が1㎝の立方体があります。
　AB,BCの真ん中の点をP,Qとするとき、三角すいB-PQFの体積は何㎤ですか。
　また、三角形PQFの面積は何㎠ですか。

　

　【ヒント】
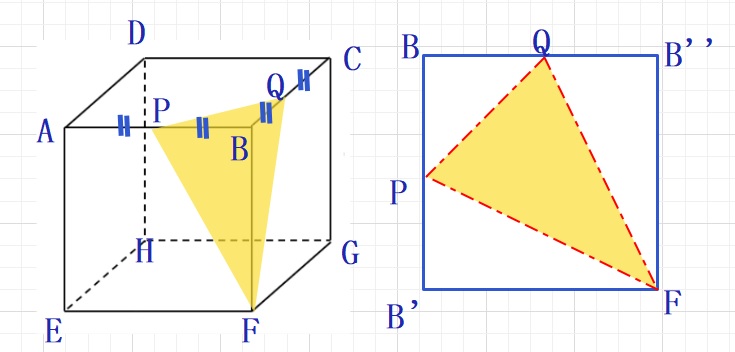
　　下の図のようにB-PQFの展開図から考えます。
　　BB’B”Fは正方形ですので、黄色い三角形の面積を求めることができそうです。
　　

【解答】
求める体積は、\(\displaystyle\frac{1}{2}\)×\(\displaystyle\frac{1}{2}\)×\(\displaystyle\frac{1}{2}\)×１×\(\displaystyle\frac{1}{3}\)=\(\displaystyle\frac{1}{24}\) ㎤・・（答え）

　△PQF=1×１－\(\displaystyle\frac{1}{2}\)×１×\(\displaystyle\frac{1}{2}\)×２－\(\displaystyle\frac{1}{2}\)×\(\displaystyle\frac{1}{2}\)×\(\displaystyle\frac{1}{2}\)

　＝１－\(\displaystyle\frac{1}{2}\)ー\(\displaystyle\frac{1}{8}\)=\(\displaystyle\frac{3}{8}\) ㎠・・・（答え）

黄色い三角形の面積は正方形の\(\displaystyle\frac{3}{8}\) 倍になります。


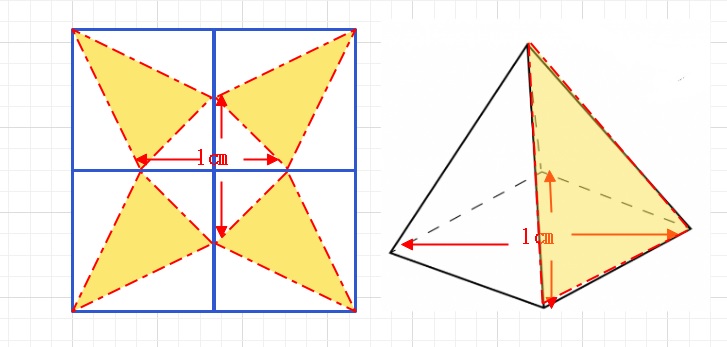
【おまけ】上で求めた三角すい４つでできる四角すいの体積は
　\(\displaystyle\frac{1}{24}\)×４＝\(\displaystyle\frac{1}{6}\)となります。
　下の展開図から計算すると、底面の正方形の面積が1×１×\(\displaystyle\frac{1}{2}\)

なので、\(\displaystyle\frac{1}{2}\)×高さ×\(\displaystyle\frac{1}{3}\)=\(\displaystyle\frac{1}{6}\) となり　高さは1㎝となります。

　 これは下の左の展開図でいうと、
　高さは展開図の大きな正方形の\(\displaystyle\frac{1}{2}\)となります。