2012年 灘中入試問題2日目4⃣より
【問題】(1)一辺の長さが1㎝の正方形の形をしたタイルをすきまなく
並べて長方形を作り、この1つの対角線に沿って切ったとき、切られたタイルの個数を数えます。
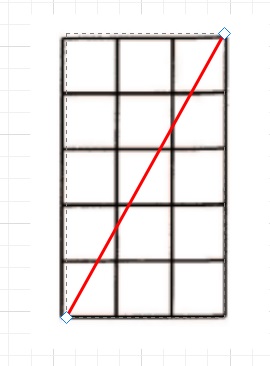
①タイル15個をたて5㎝、よこ3㎝の長方形に並べたとき、切られたタイルは ア個です。
②タイル5184個をたて81㎝、よこ64㎝の長方形に並べたとき、切られたタイルは何個ですか。
③タイル11664個をたて144㎝、よこ81㎝の長方形に並べたとき、切られたタイルは何個ですか。
(2)1辺の長さが1㎝の立方体の形をした透明なブロックを、
すき間なく並べて直方体を作ります。この直方体の1つの頂点から
残り7つの頂点の中で、最も遠い頂点に向かって、光線を発射します。
光線はまっすぐ進み、ブロックによって反射したり、方向が変化したりすることは
ありません。この光線がつらぬいているブロックの個数を数えます。
ただし、光線がブロックの頂点のみを通っている場合や、
辺のみを通っている場合には光線はブロックを貫いているとは考えません。
ブロック202500個を縦75㎝、よこ90㎝、高さ30㎝の直方体に並べたとき
つらぬかれたブロックは何個ですか。
【ヒント】こちらを合わせてご確認下さい。★★★☆☆難関コース 立体のくしざし | 算数コロシアム (mathcolo.com)
まずは簡単な例から考えます。①は横に2枚のかべ、たてに4枚の壁を突き抜けていきいます。
②も同様に考えますが、81=3×3×3×3、64=2×2×2×3ですので
とちゅう一度もかどをとおることなく、最後の頂点までたどり着き、①と同様にとけます。
③は144=12×12=2×2×2×2×3×3、81=3×3×3×3となり、最大公約数は9
なので、たて16㎝、横9㎝でカドをとおり、これを9回繰り返すこととなります。
(2)75=5×5×3、90=3×3×2×5、30=5×2×3ですので、最大公約数は15となり
たて5㎝、横6㎝、高さ2㎝の直方体が15セットあると考えます。
この場合、5,6,2の最小公倍数30を基準に、それぞれをくぎると、
たて 6,12,18,24 横 5,10,15,20,25 高さ 15
となり、かべは 5,6,10,12,15,18,20,24,25 の9枚を通過することとなります。
【解答】(1)①2+4+1=7・・・アの答え
②80+63+1=144個・・(答え)
③(15+8+1)×9=216個・・(答え)
(2)(9+1)×15=150個・・・(答え)

コメント