難易度
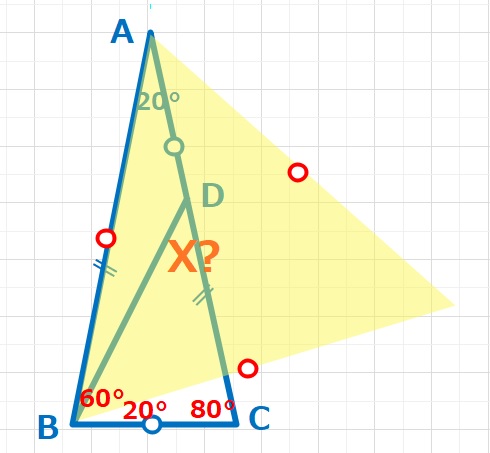
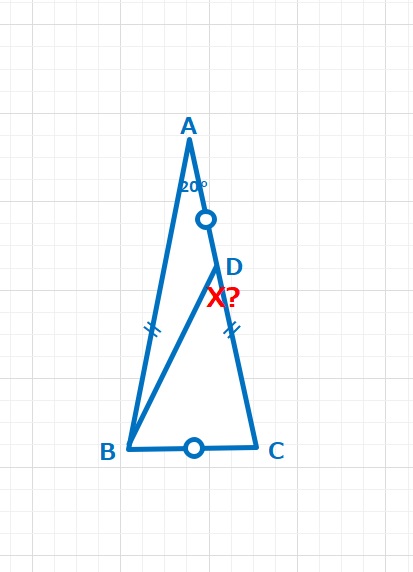
三角形ABCは∠BAC=20°,AB=ACとなる二等辺三角形です。AD=BCのとき、X=∠BDCは何度ですか。
【ヒント】とても興味深い問題です!今回は2パターンのアプローチ(解法)を紹介します。与えられた条件で、BC=ADを何とか活用したいのですが、少し離れてて、なかなかイメージがわきません(笑)
しかし、20°の三角形は正三角形や二等辺三角形と相性がよく、またラングレーの最初の問題で有名な正18角形(20°の二等辺三角形を360°÷20=18個組み合わせた正多角形)の対角線問題に挑戦したことがある人なら、簡単かもしれません。少し難しめの角度の問題を克服したい人はぜひチャレンジしてほしいです。
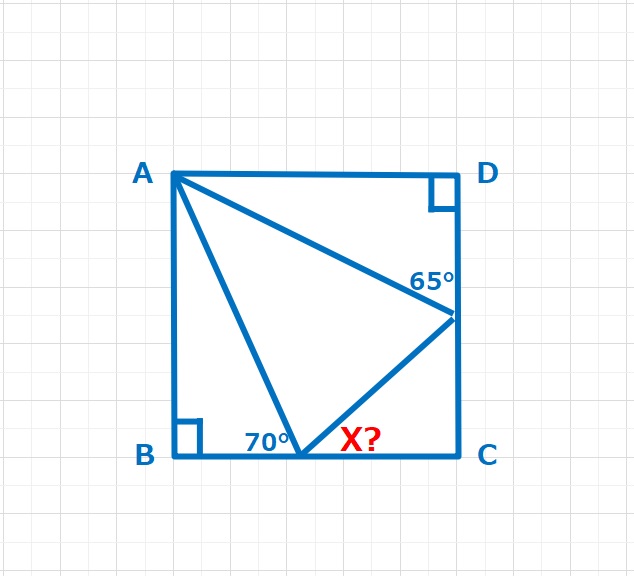
まず下図のような正三角形を書いてみます。
下図のように点Eをとると△DABと△CBEは二辺とその間の角(∠DAB=∠CBE=20°,AB=BE,AD=BC)が等しいので合同な三角形となります。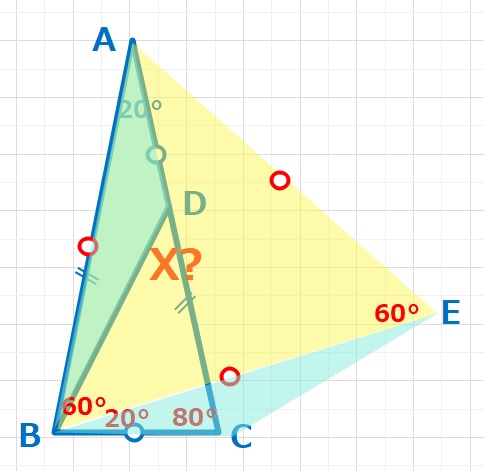
【解答1】
ABを1辺とする正三角形ABEを作る。△ACEはAC=AEなので ∠CAE=40°の二等辺三角形となります。△CEBに注目して ∠BCE=∠ADB=150°(ヒント参照)となり、X=∠BDC=180-150=30° ・・・(答え)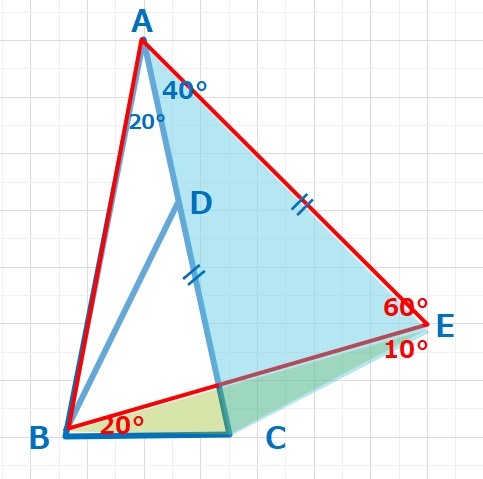
【解答2】
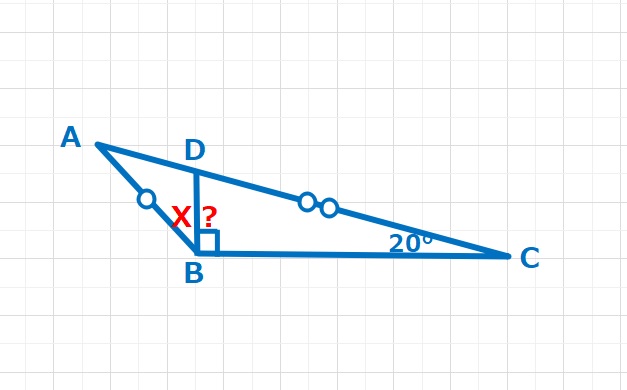
実は最初に思いついた解答はこちらで、対称な図形を作り、隠れた正三角形をみつけ、合同な図形を作りました。少し小さいですが、BCを1辺とした正三角形FBCとなる点Fをとり、BFの延長線上でACとの交点をGとします。そうすると、∠ABF=∠ACF=∠CDF=∠DGF=20°△GABは二等辺三角形となり∠AGB=140°とります。△FCDも二等辺三角形となり、FD=FC=BC=ADとなり、△DAFと△FDCも二等辺三角形となります。∠DAFは10°なので∠BDF=10°となり∠BDC=30°・・・(答え)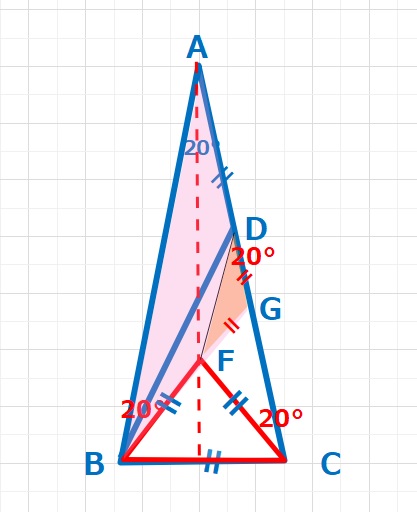
おまけ
この問題の元ネタは下図の正18角形となります。
正18角形の対角線のなかに今回の問題が隠れていました。△O(P7)(P0)は140°,20°,20°の二等辺三角形となり、△F(P1)(P0)は正三角形となります。
同様に、△O(P8)(P0)は160°,10°,10°の二等辺三角形となり、これが今回の問題のBDにあたります。奥が深いですね!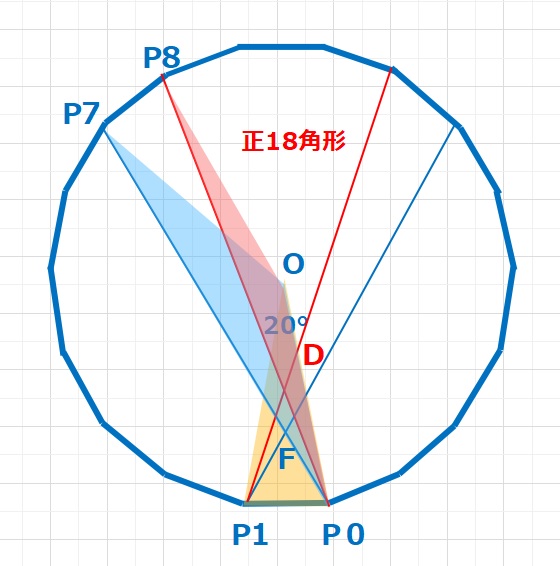
コメント