難易度
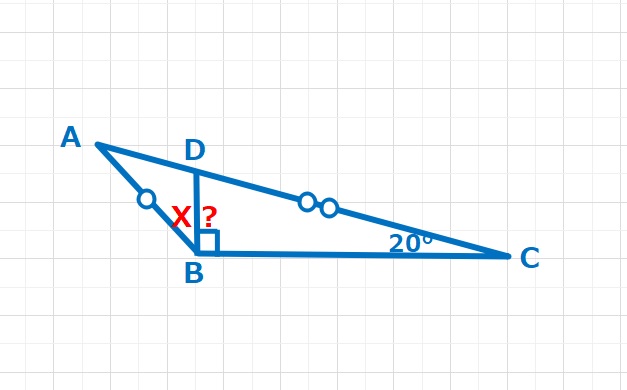
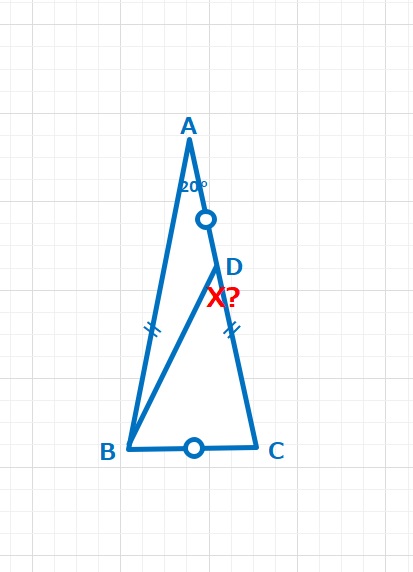
∠DBC=90°,∠ACB=20°,DC=2×AB(DCはABの2倍の長さ)となる△ABCがあります。X=∠ABCは何度ですか。
【ヒント】DCの中点をEとし、BC,DBそれぞれにEから垂直に下した線の交点をF,Gとします。△DGEと△DBCに注目すると、2つの三角形の3つの角度は等しいので相似な関係にあります。よって DG=GB=EFとなります。(四角形GBFEは長方形)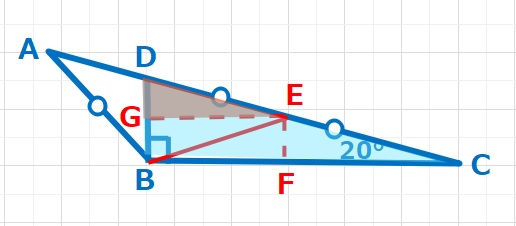
同様に△CEFと△CDBに注目すると、2つの三角形の3つの角度は等しいので、相似な三角形となります。よって BF=FC=GEとなります。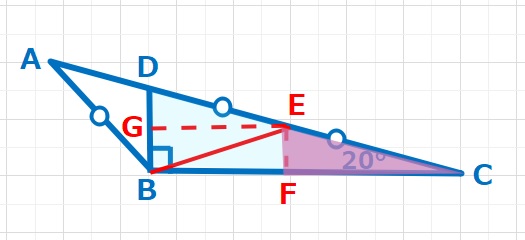
【解答】
DCの中点をFとすると、△FBCは二等辺三角形なので、∠FBC=20°
よって∠DFB=∠FBC+∠FCB=40°となります。
また、△FDBも二等辺三角形なので∠FDB=\(\displaystyle\frac{180-40}{2 }\)=70°となります。
∠DAB+∠DBA=70°なので、
X=∠DBA=70-40=30°・・・(答え)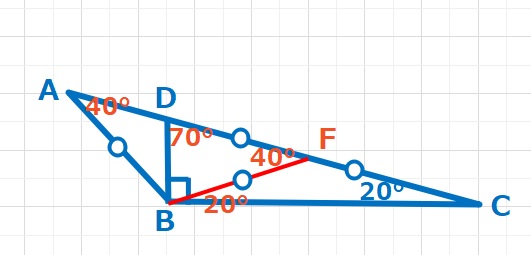
コメント