難易度
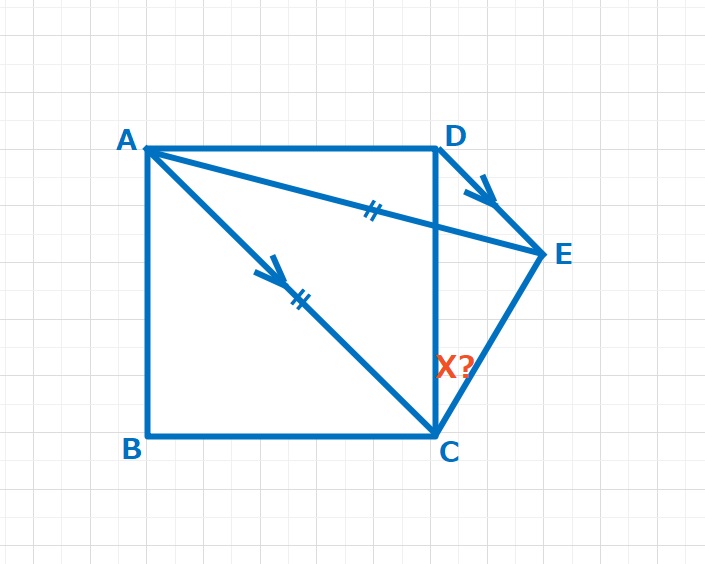
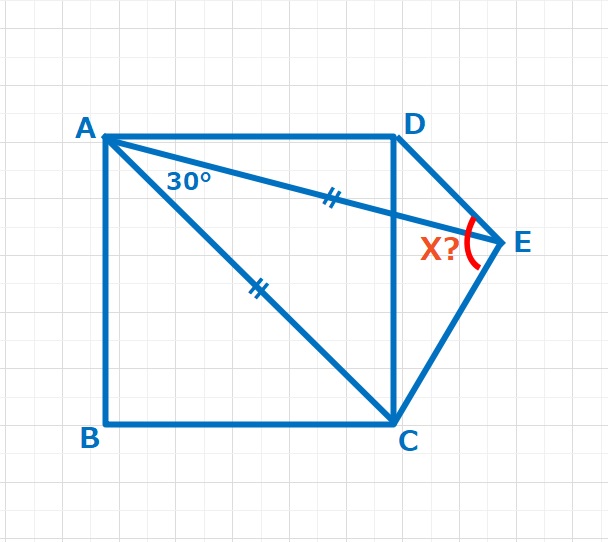
正方形ABCDに対しAC=AE,DEとACが平行になるように点Eをとります。Xは何度ですか。
【ヒント】 与えられた情報をまず整理します。
角度の情報がほぼありませんが、、方眼問題三部作①②を解いたかたなら、、なんとなく∠CAEは30°なのかなと、(笑)想像できます。
ほぼ角度の情報がないので、なんとか突破口を、、対称な図形を作るために、対角線BDを書き、ACとの交点をFとします。AF=FC=BF=DFとなり点EからACに垂線EGをおろすと四角形DFGEは長方形なのでDF=EGとなります。そうすると少し、突破口が見えてきました。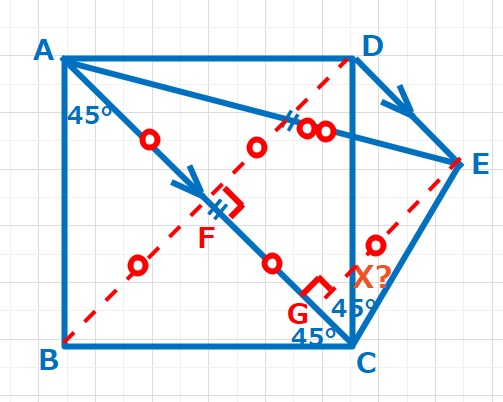
【解答】
対角線ACとDBの交点をF, 点EからACに下した垂線の足をGとすると、
DF=EG,またAC=AE=2×EGとなるので三角形EAGは∠EAG=30°のEG:AE=1:2の直角三角形となる。∠AEG=60°となり、また∠AEC=\(\displaystyle\frac{180-30}{2 }\)=75° よってX=∠ECD=75-45=30° ・・・(答え)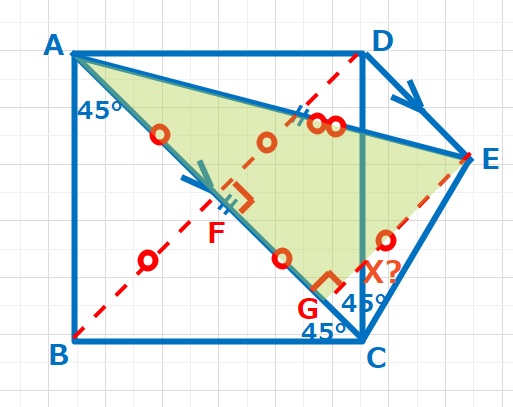
コメント