難易度
算数オリンピック2021年 トライアル
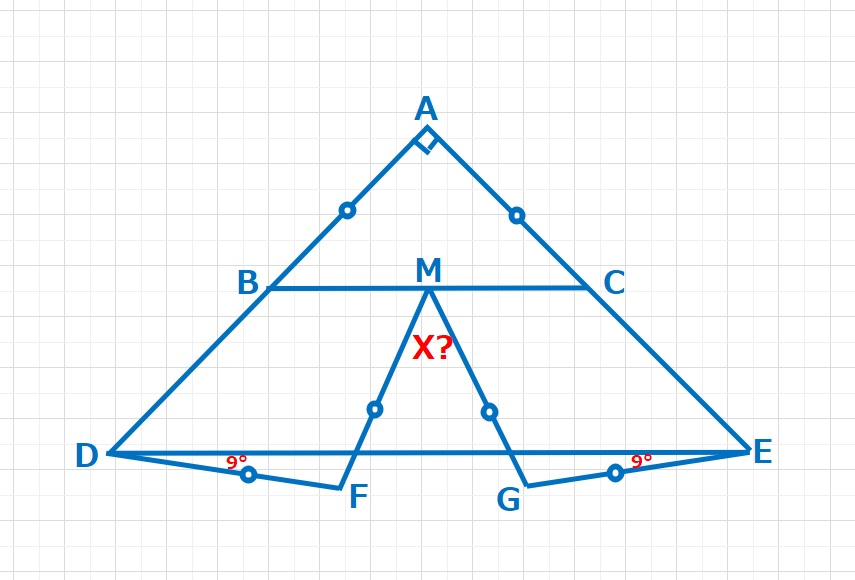
【問題】△ABCと△ADEは∠A=90°の直角二等辺三角形で、点MはBCの中点です。いま、AB=AC=DF=FM=EG=GMとすると、∠FDE=∠GED=9°となりました。X=∠FMGの大きさは何度ですか。ただし、図は正確とは限りません。
【ヒント】糸口がなかなか見つかりませんが、気づけば一瞬で解けてしまいます。
ヒントは45°と ∠ADF=54°情報くらいしかなく、あとは長さ情報から正三角形や二等辺三角形を探し出すしかないのですが、、54°から正五角形をイメージするしかなさそうです。
△ABCの情報の代わりにせめて、△MJKの情報が与えられていればもう少し気づきやすいのですが。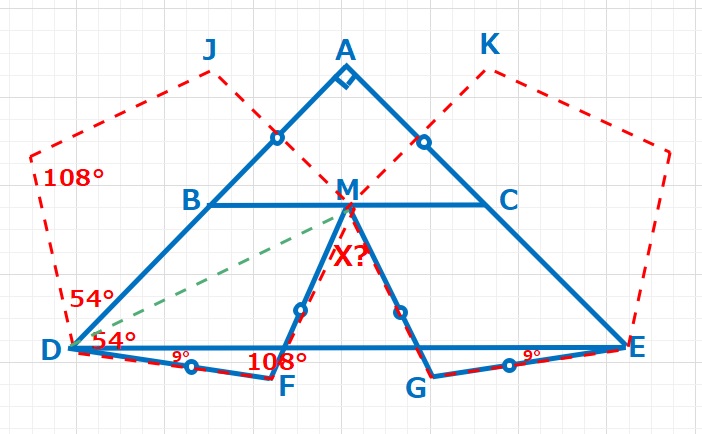
【解答】二等辺三角形MDEに注目して、∠MDE=∠MED=27°なので∠DME=126°
∠DMF=∠EMG=36°なので、X=∠FMG=126-(36+36)=54°・・・(答え)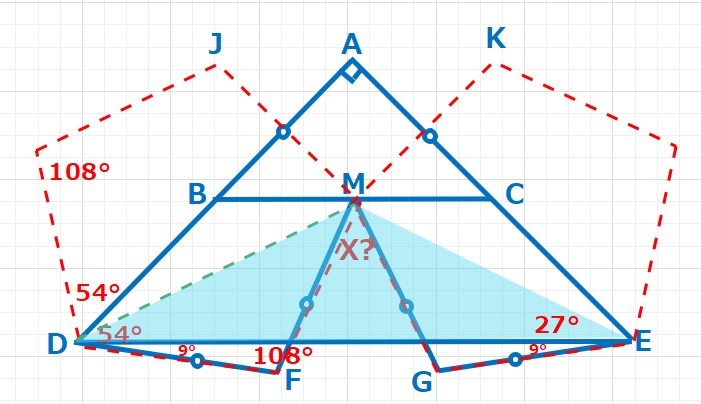
コメント