難易度
2018年ジュニア算数オリンピック ファイナル問題
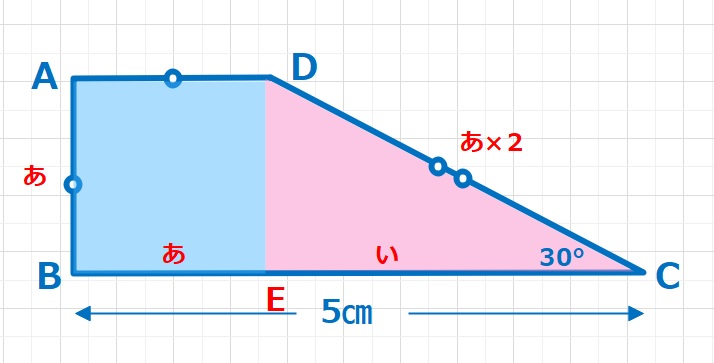
【問題】AB=AD,∠C=30°であるとき、台形ABCDの面積を求めなさい。
【ヒント1】台形を1辺が「あ」の正方形ABED(ブルー)と30°,60°,90°の直角二等辺三角形CDE(ピンク)に分解します。ECの長さを「い」とすると、「あ」+「い」=5㎝、DCは「あ」×2㎝となります。
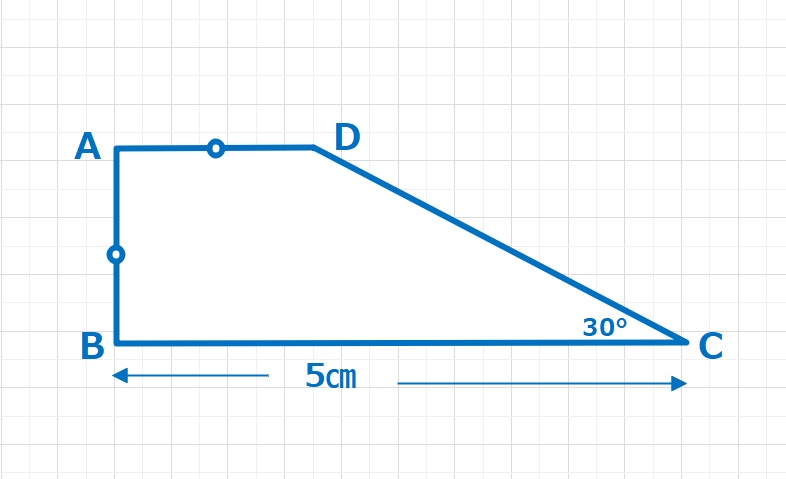
【ヒント2】与えられた台形を下図のように変形します。
【解答】与えられた図形を変形し、同じものを下図のように4つ組み合わせます。
「あ」+「い」=5㎝なので求める台形の面積は、一辺が5㎝の正方形の面積の\(\displaystyle\frac{1}{4}\)となります。
よって、 \(\displaystyle\frac{5×5}{4}\)=6.25㎠・・・(答え)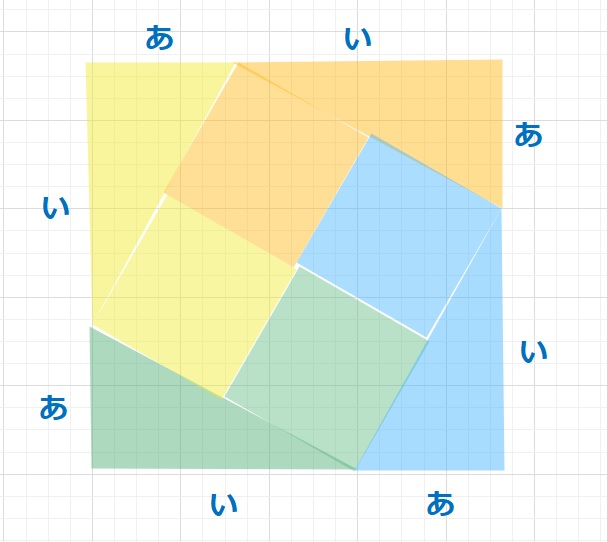
コメント