ある日、妻より算数の図形問題を出題されました。実はその問題、1972年の灘中の中学入試問題として出題された問題で、解くのに無茶苦茶時間がかかり、がく然としました。そして、これがラングレーの最初の問題とよばれていることを知り、斉藤先生の「ラングレーの問題にトドメをさす!」という本を買ったことが、このブログを書くきっかけとなりました。
ラングレーの問題の始まりは、Edward M.Langleyが、The Mathematical Gazette誌1922年10月号のMathematical notesというショートコラム欄に掲載した ‘A Problem’というタイトルのたった2行の記事でした。
ABC is an isosceles triangle.B=C=80°.CF at 30° to AC cuts AB inF.
BE at 20° to AB cuts AC in E.Prove ∠BEF=30°.
訳)△ABCは二等辺三角形で、∠B=∠C=80°。直線ACと30°をなす直線CFは線分ABと点Fで交わり、直線ABと20°をなす直線BEは線分ACと点Eで交わる。∠BEF=30°を証明せよ。
斉藤 浩 著 「ラングレーの問題にトドメをさす!」現代数学社より引用
ラングレーの問題ー4点角問題ー
下図のa,b,c,d,Xの値がすべて整数となるような四角形のことを一般に整角四角形と呼びます。またa,b,c,dの角度を与えてXを求める問題をラングレーの問題または整角四角形の問題と呼ぶそうです。
この問題をL(a,b,c,d)と表すことにします。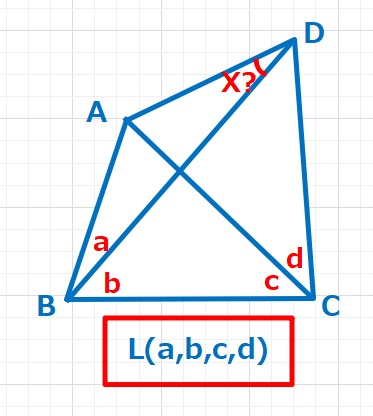
同様に4つの点のうちの3つが作る三角形の内部にもう1点がある場合で、この4点が作る角度が全て整数となるものを、一般に整角三角形とよび、a,b,c,dの角度を与えてXを求める問題を整角三角形の問題と呼びます。この問題をT(a,b,c,d)と表すことにします。そしてこの両方の問題を合わせて4点角問題と呼ぶようです。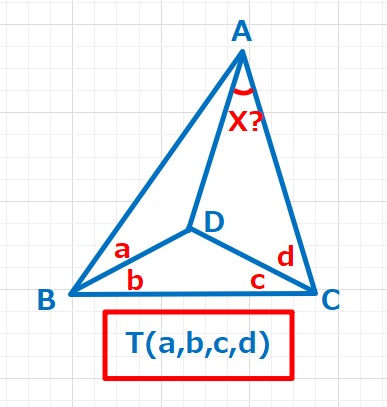
コメント