難易度
算数オリンピックファイナル問題
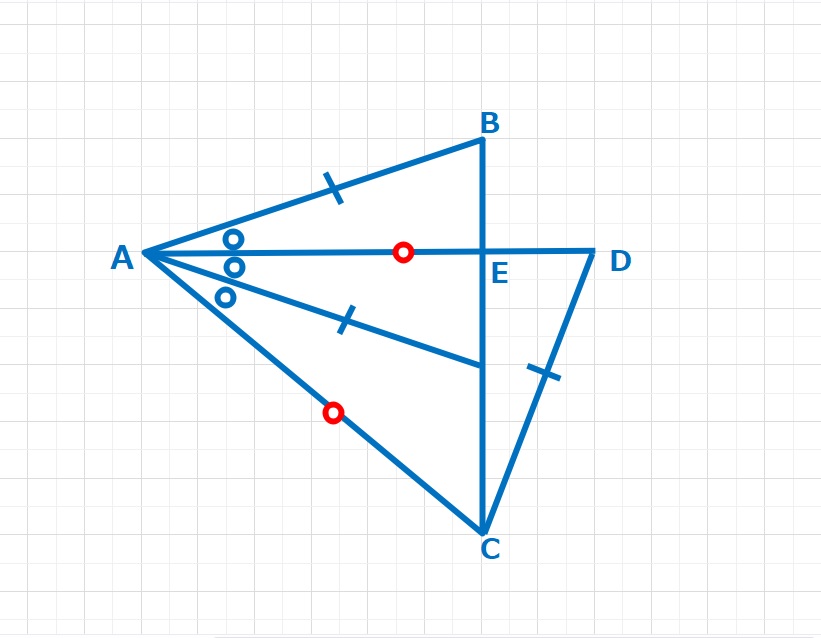
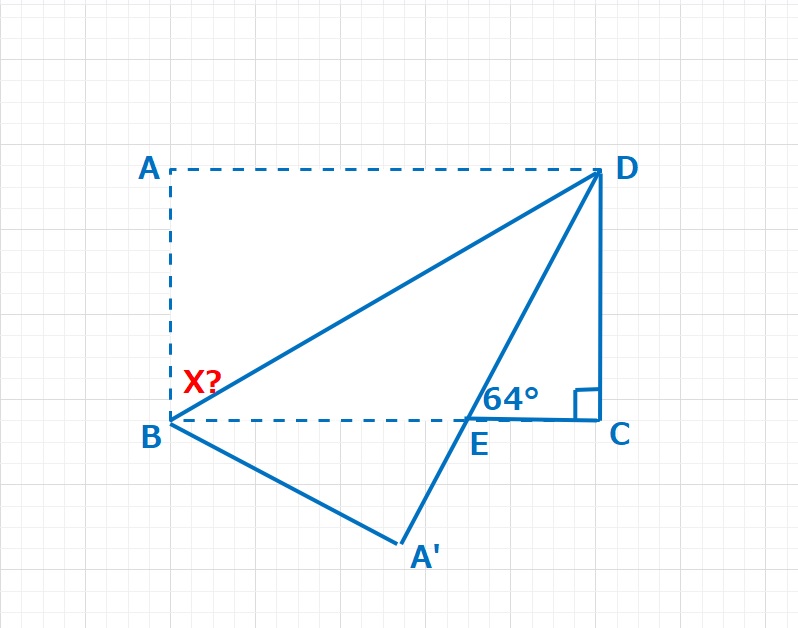
【問題】三角形ABCの角BACの3等分線をAD,AFとする。ADとBCの交点をEとすると、AB=AF=CD,AD=ACとなった。このとき、角BACの大きさを求めなさい。
【ヒント】∠ABE=×とすると、「〇」+「×」=90°, AD=ACなので、△ADCは二等辺三角形となり、∠ADC=×となります。△ABEと△CDEにおいてAB=CD,∠BAE=∠DCE,∠ABE=∠CDEなので1辺とその間の角が等しいため、合同な三角形となります。
よて EA=ECとなります。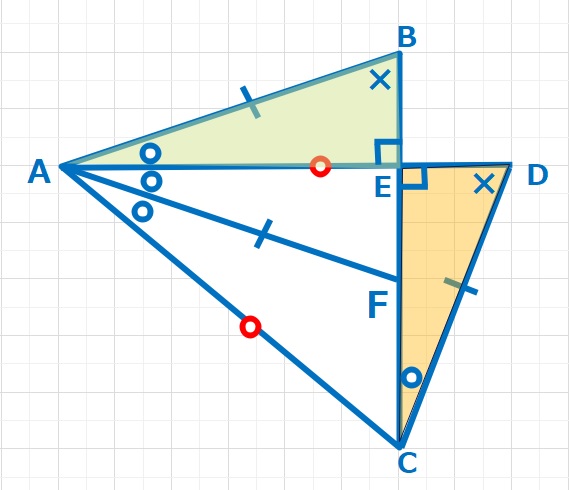
【解答】EA=ECより△EACは ∠AEC=90°の直角二等辺三角形。よって 〇〇=45°なので、〇1つは22.5°となります。 ∠BAC=22.5×3=67.5°・・・(答え)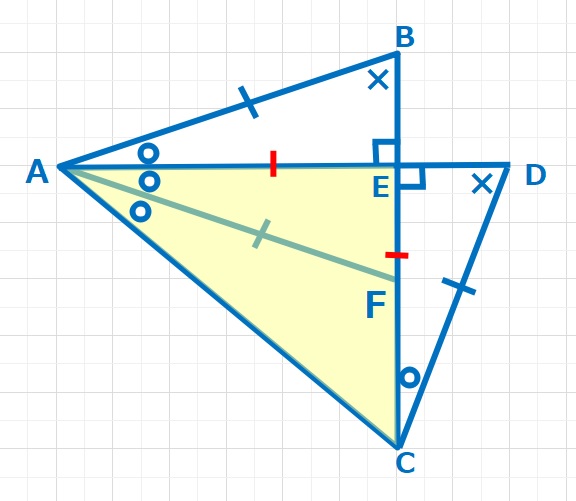
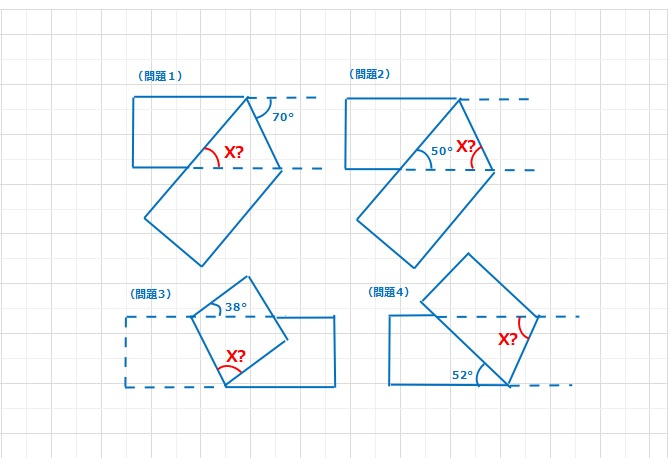
コメント