 角度の問題
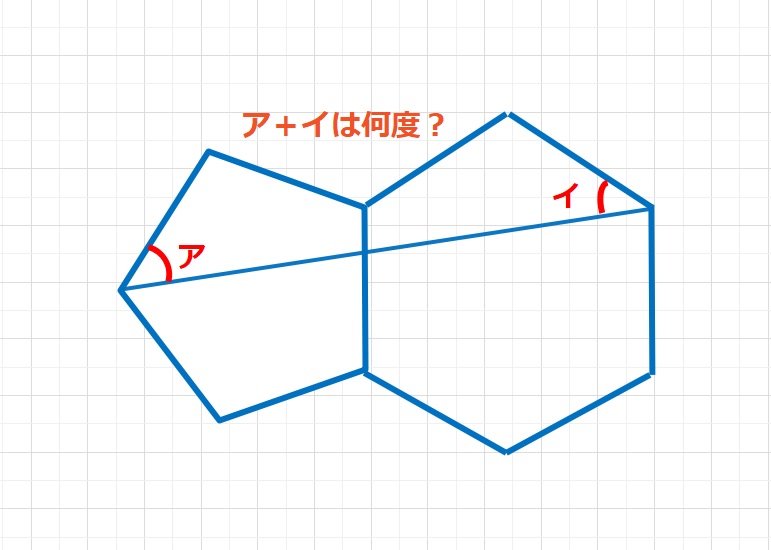
角度の問題 ★★☆☆☆中級コース 基本図形の組み合わせLV5
難易度1辺が同じ長さの正五角形と正六角形があります。アとイの合計の角度は何度でしょうか。【ヒント1】正五角形は \(\displaystyle\frac{180}{5}\)=72°を頂角とした二等辺三角形を5個組み合わせてできています。正...
 角度の問題
角度の問題 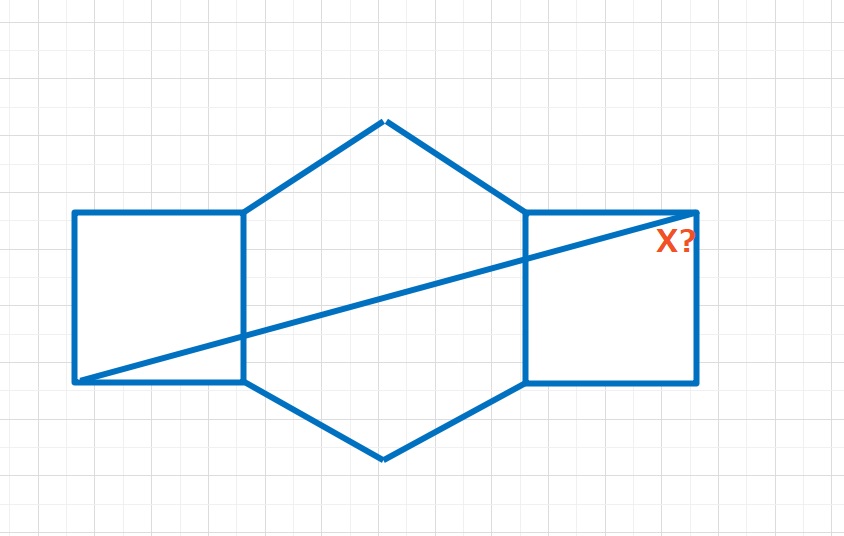 角度の問題
角度の問題 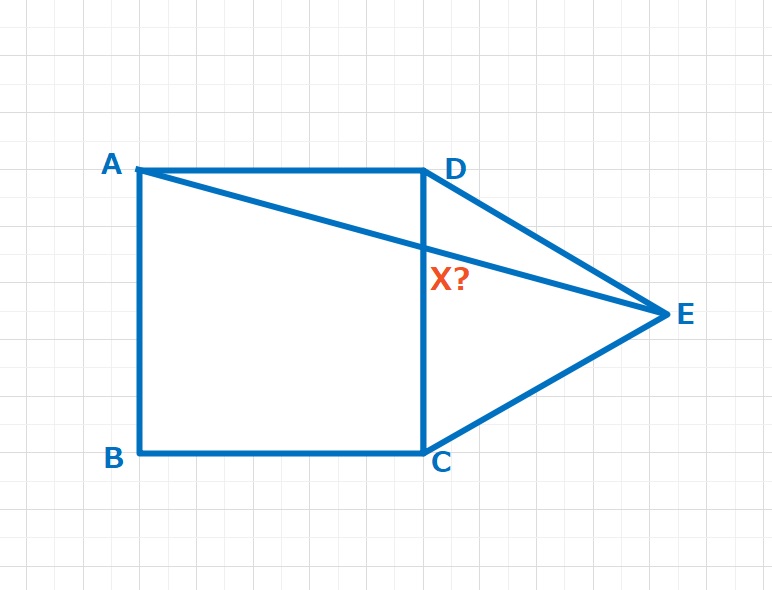 角度の問題
角度の問題 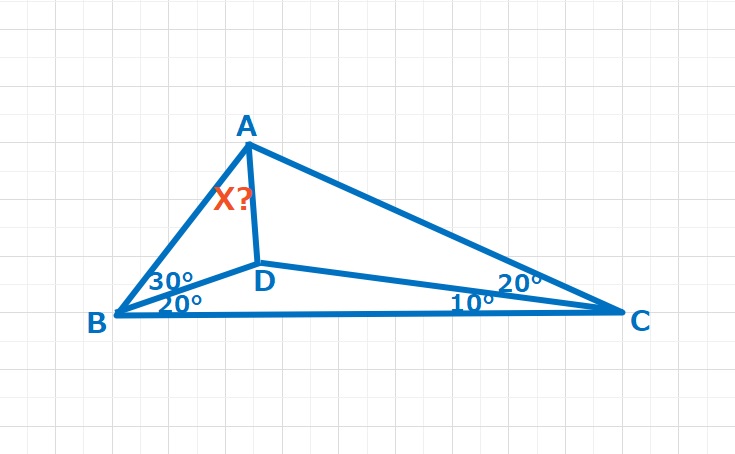 ラングレーの問題
ラングレーの問題 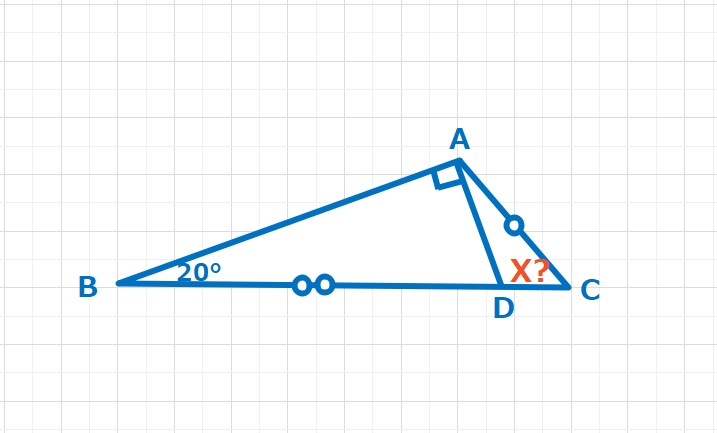 図形
図形 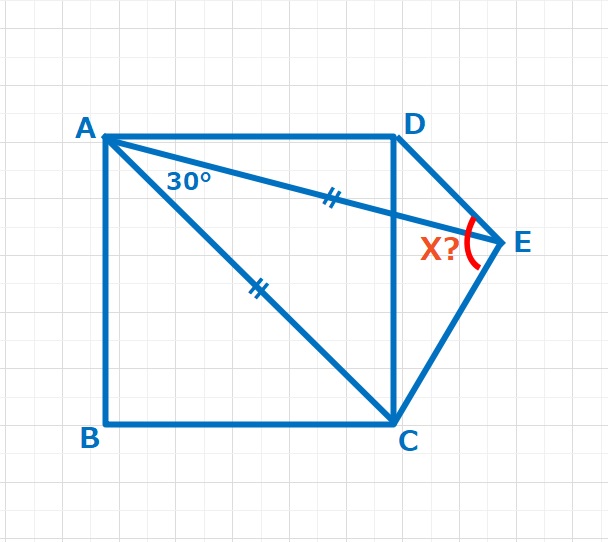 ラングレーの問題
ラングレーの問題 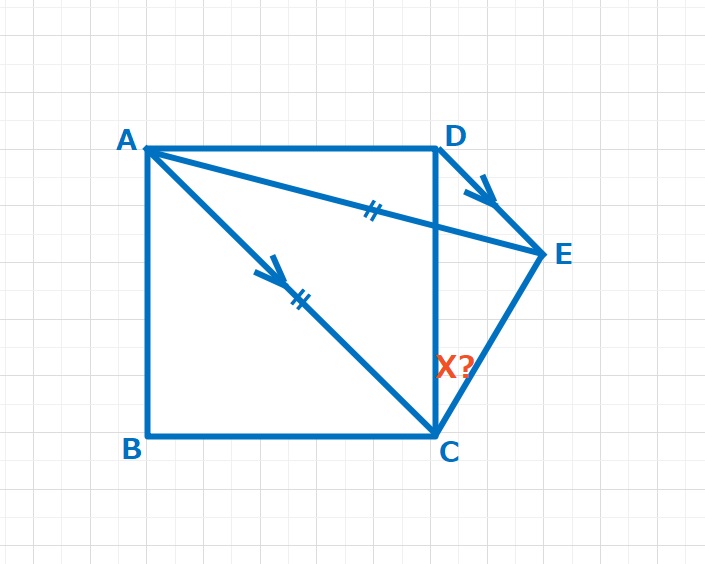 図形
図形 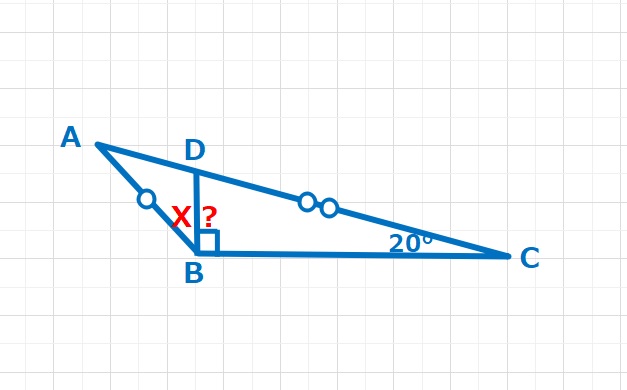 角度の問題
角度の問題 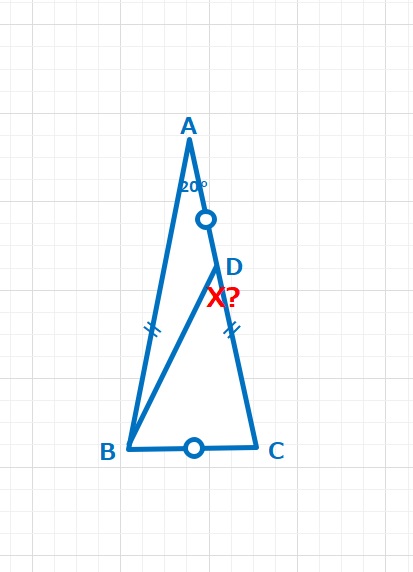 角度の問題
角度の問題 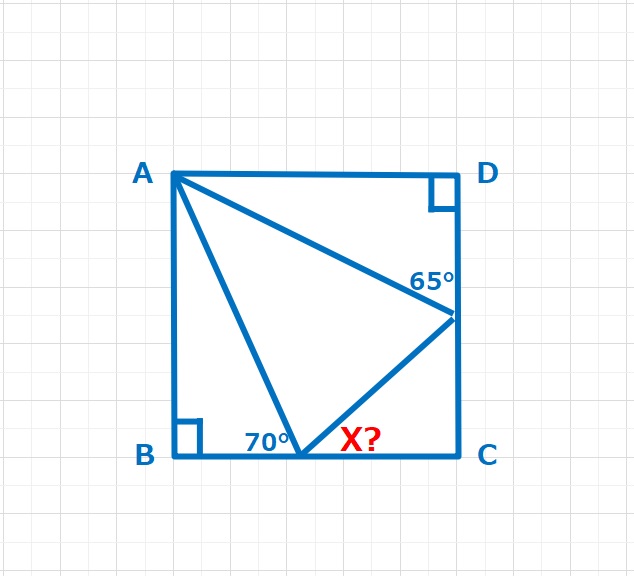 図形
図形 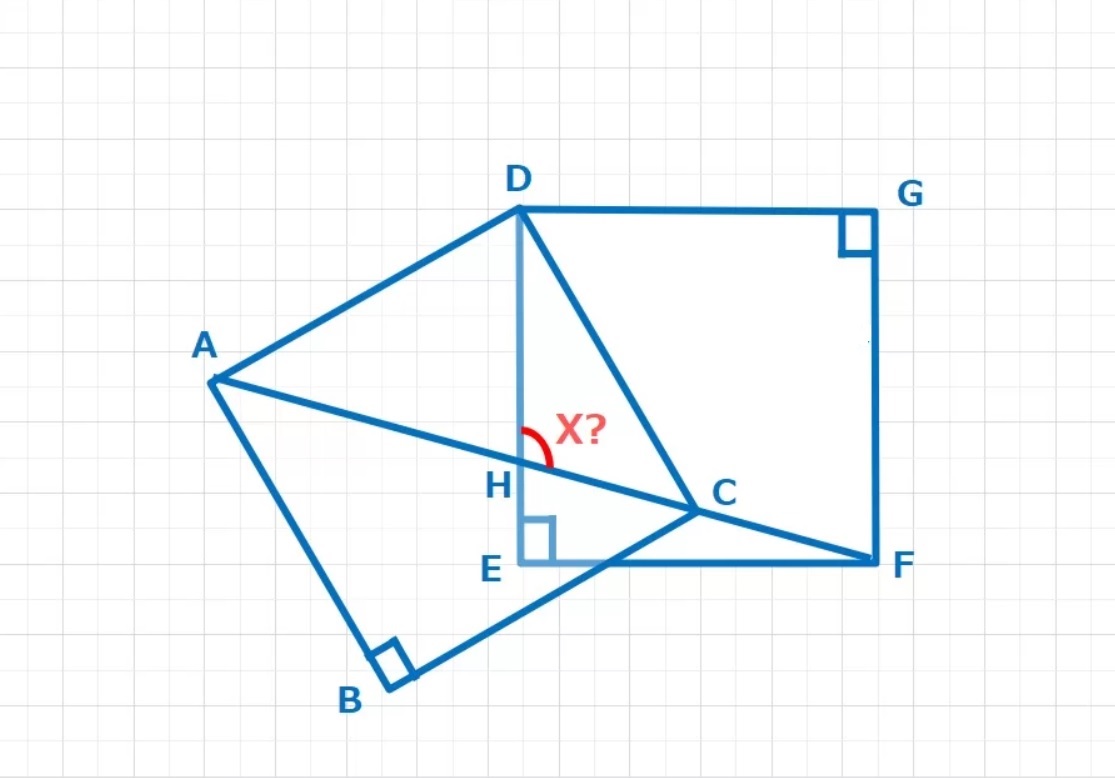 図形
図形 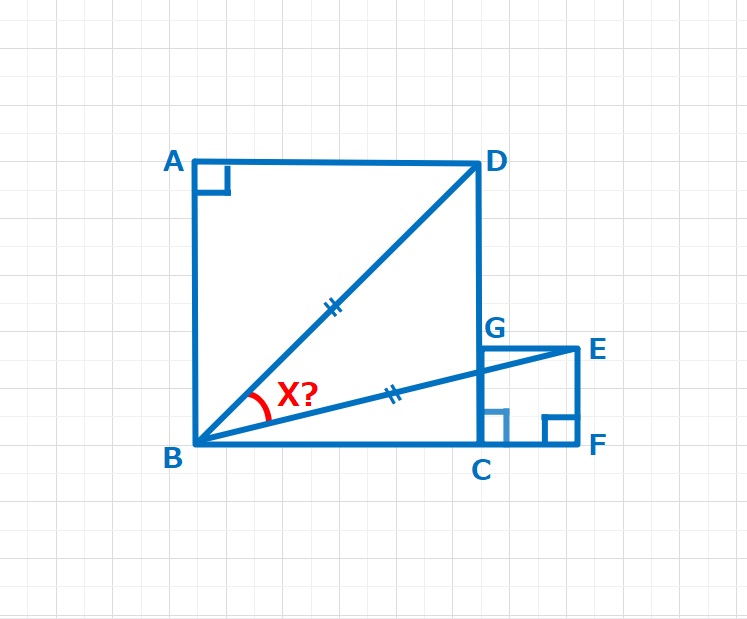 図形
図形 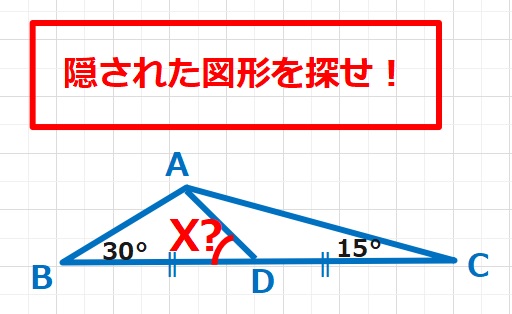 図形
図形 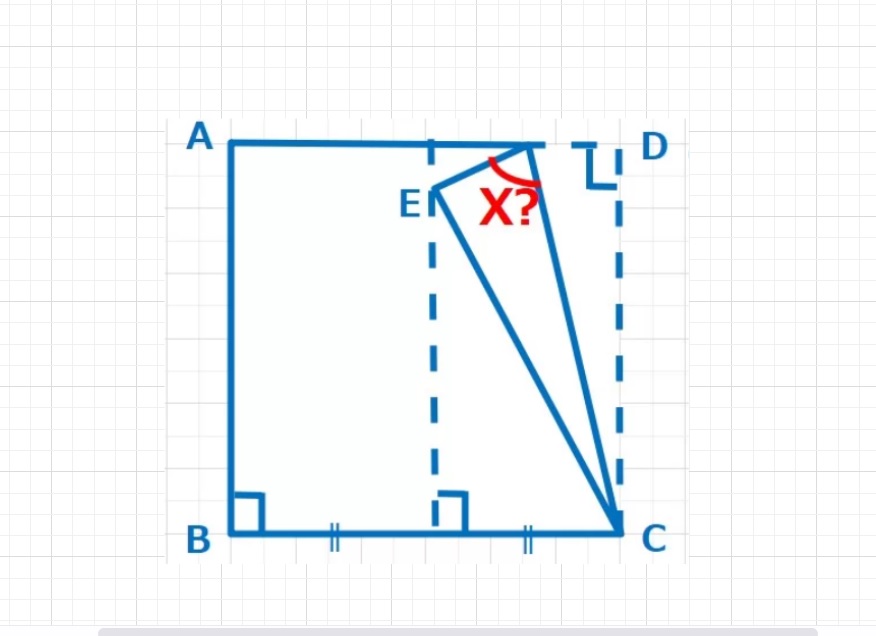 図形
図形 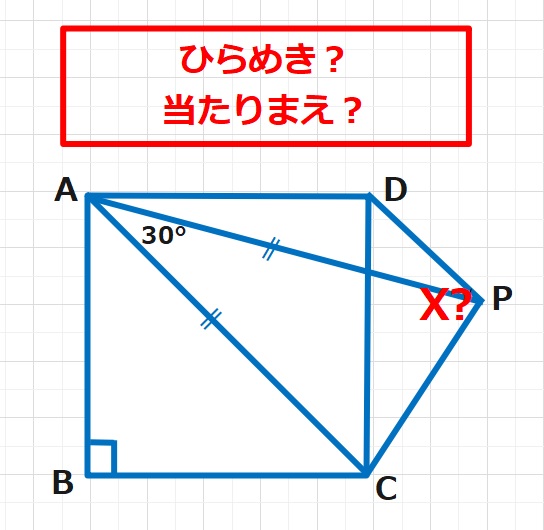 図形
図形 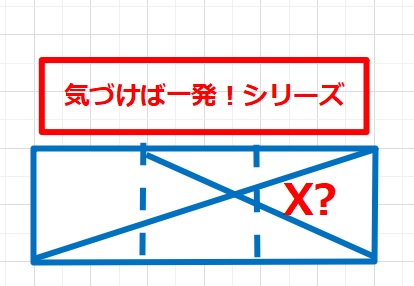 図形
図形 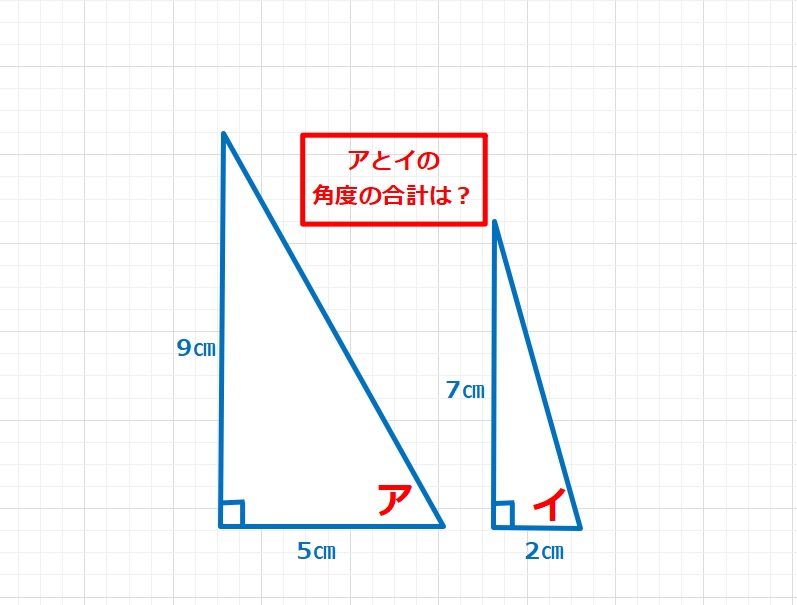 図形
図形 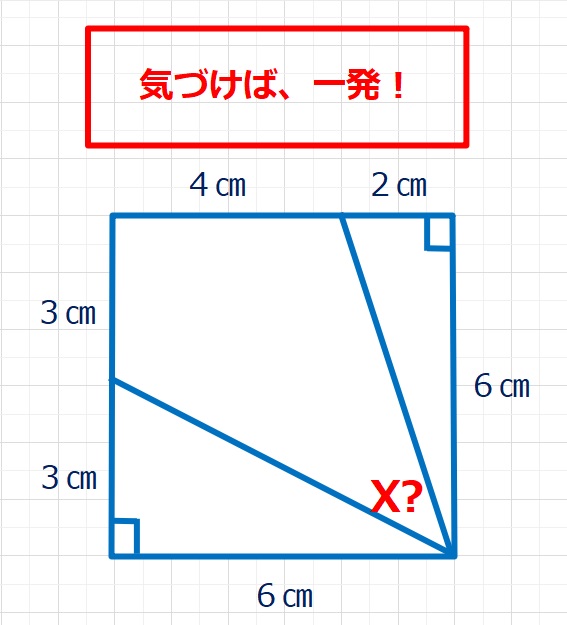 図形
図形 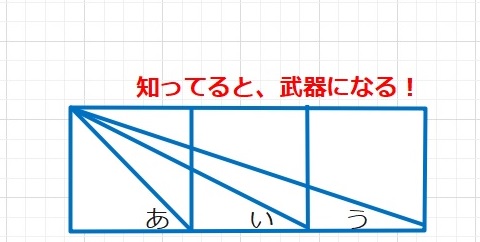 図形問題の武器
図形問題の武器 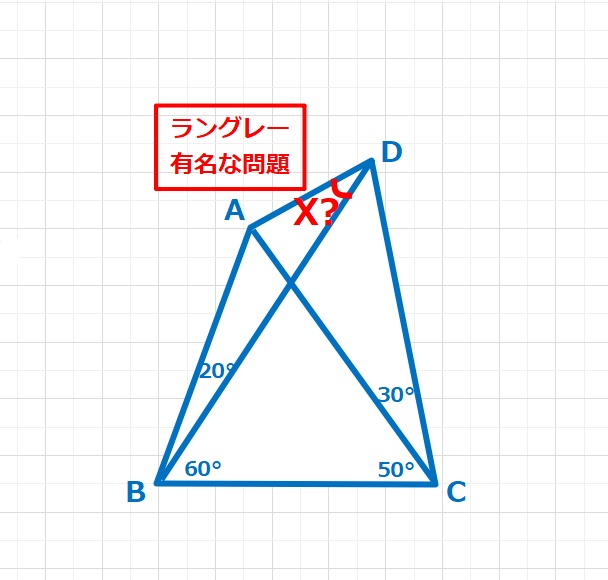 ラングレーの問題
ラングレーの問題