 図形
図形 ★★☆☆☆難関コース 灘中入試問題。与えられた長さの条件をどのように活用するかがポイント。
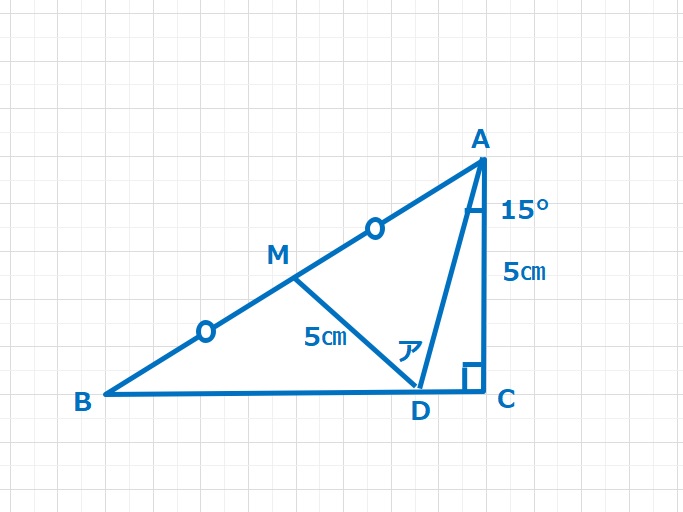
難易度2013年 灘中入試問題【問題】直角三角形ABCで、Mは辺ABの真ん中の点です。また∠DAC=15°で、ACとMDの長さはともに5㎝です。この時、アの角の大きさは何度ですか。また、BDの長さは何㎝ですか。図は正確とは限りません。
...
 図形
図形 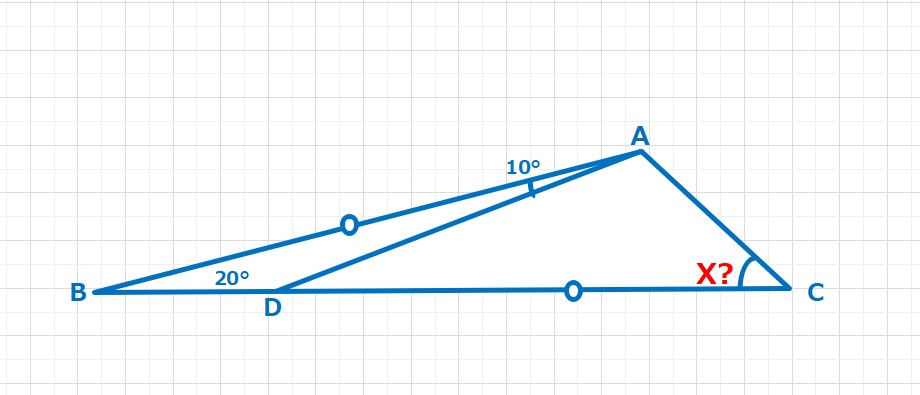 図形
図形 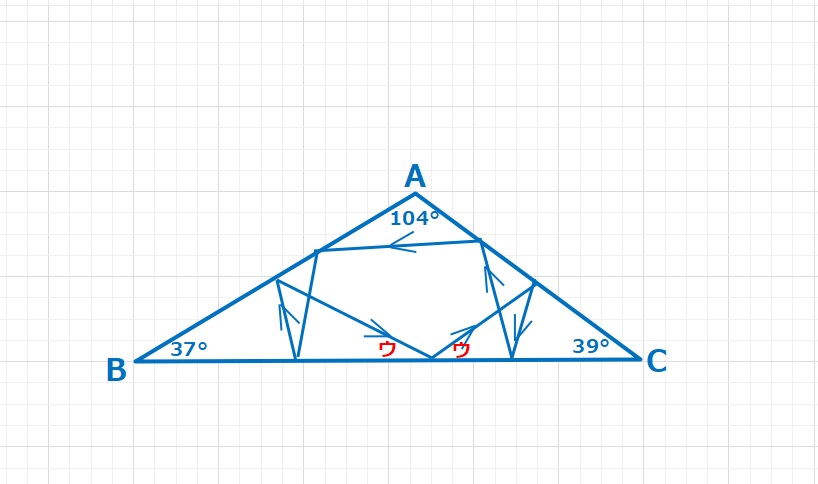 図形
図形 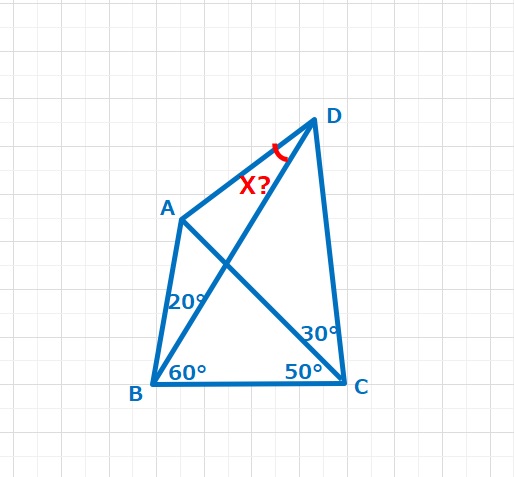 ラングレーの問題
ラングレーの問題 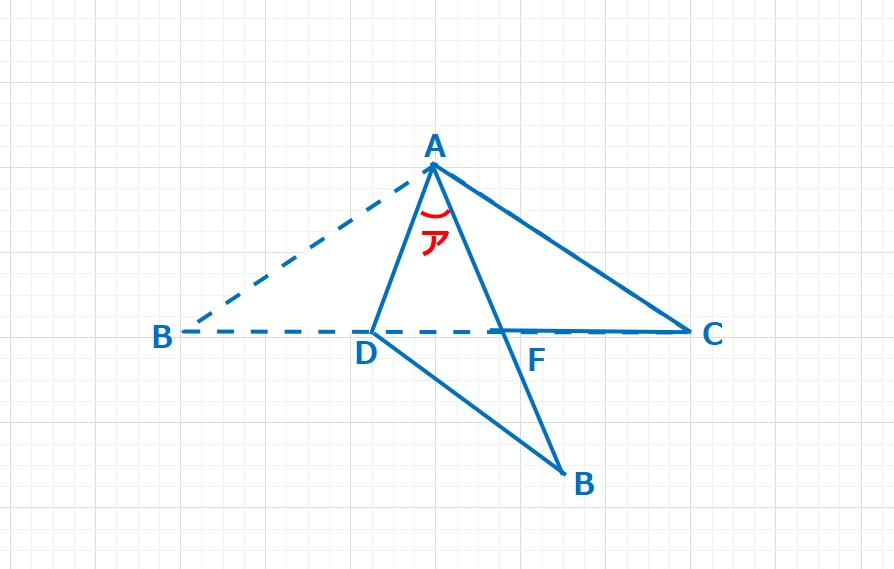 図形
図形 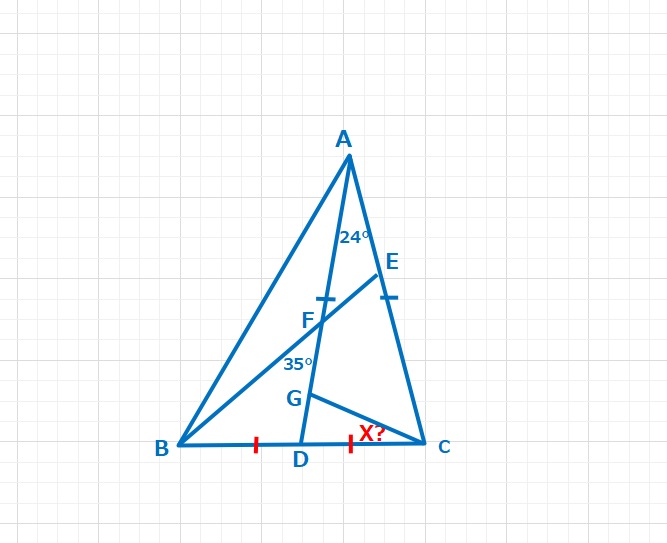 図形
図形 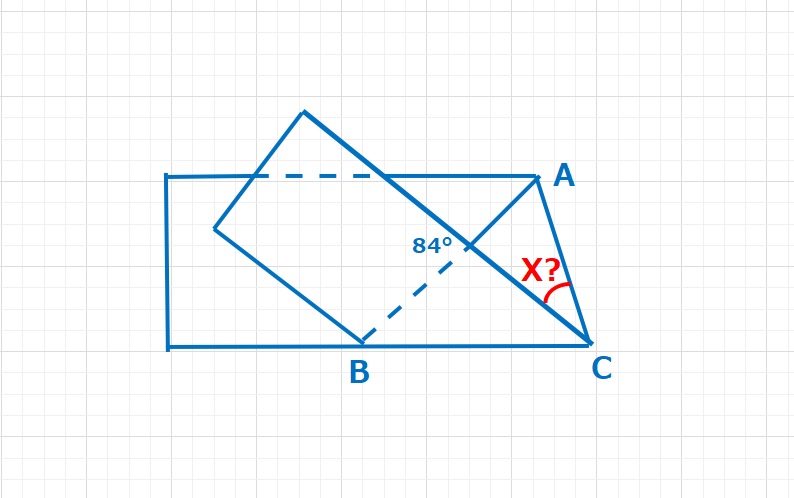 図形
図形 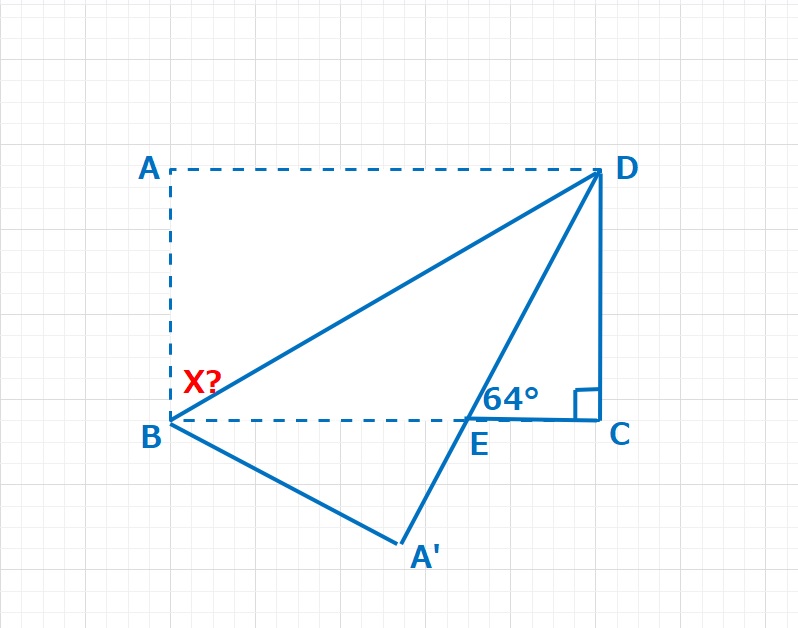 図形
図形 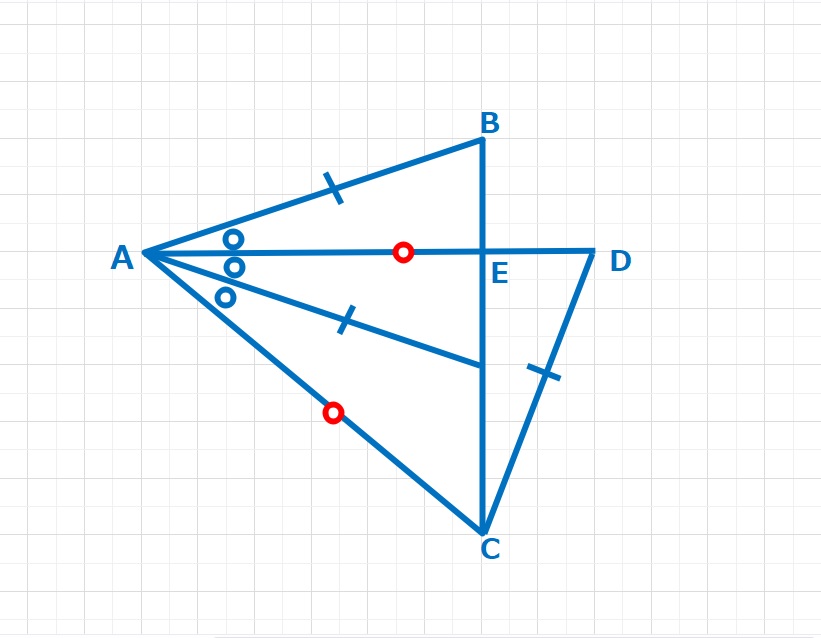 図形
図形 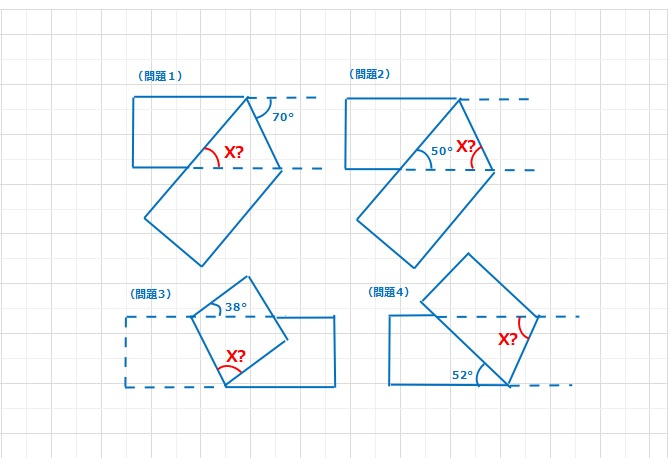 図形
図形 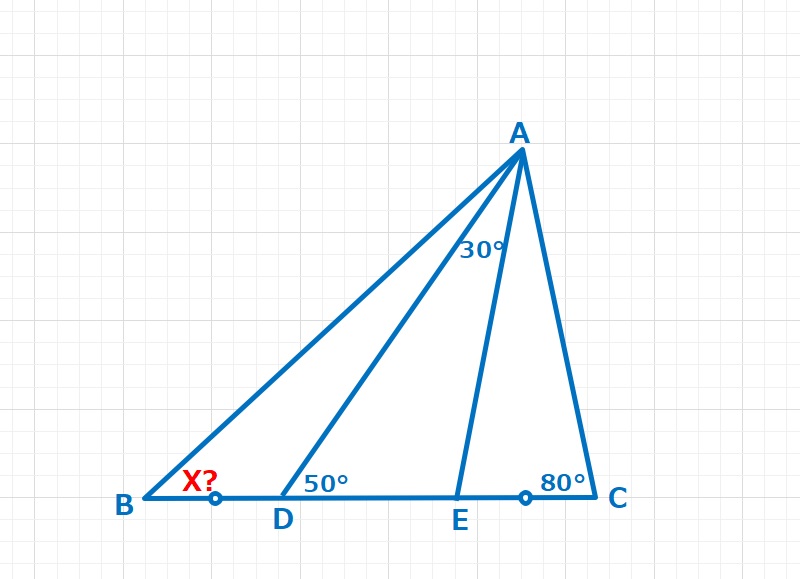 図形
図形 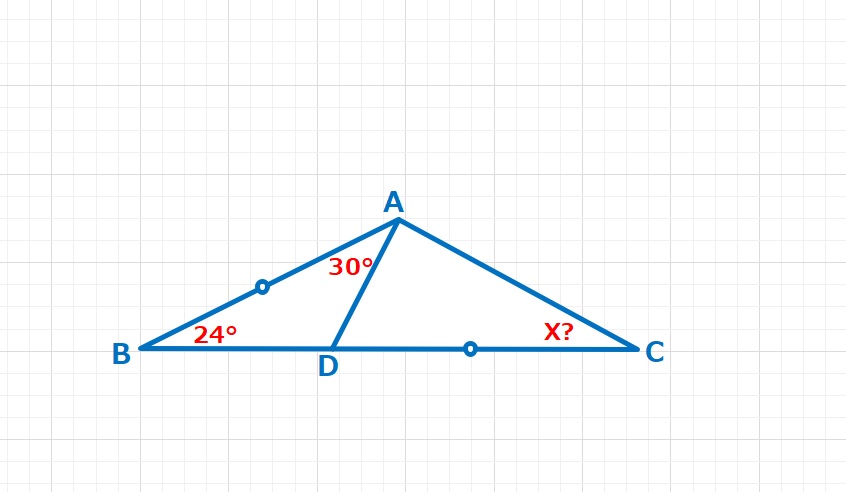 図形
図形 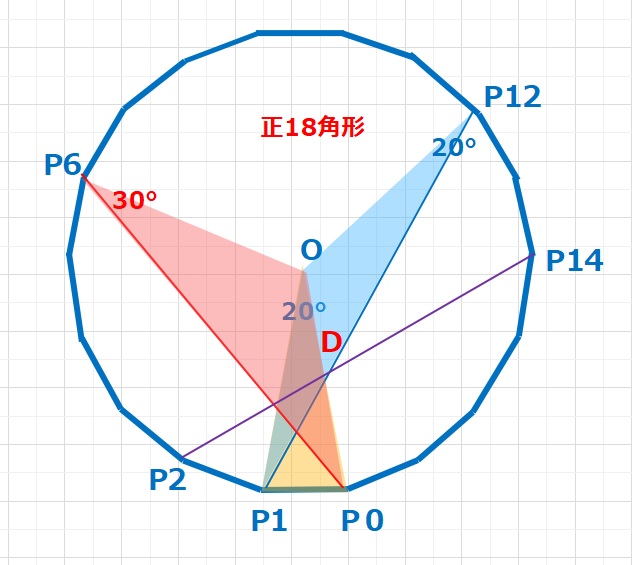 コラム
コラム 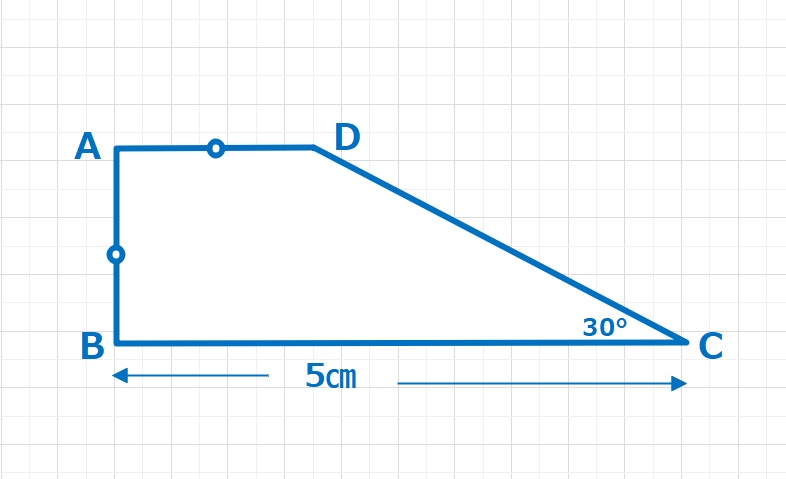 図形
図形 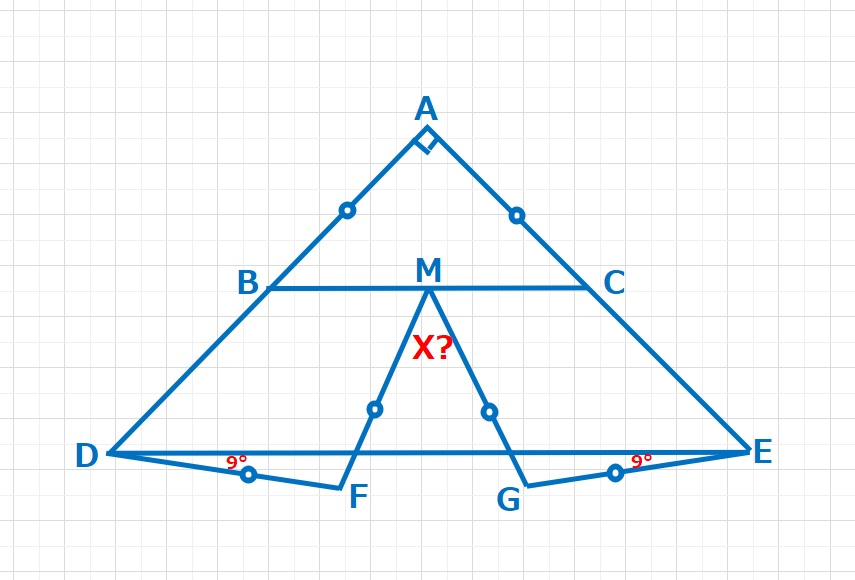 図形
図形 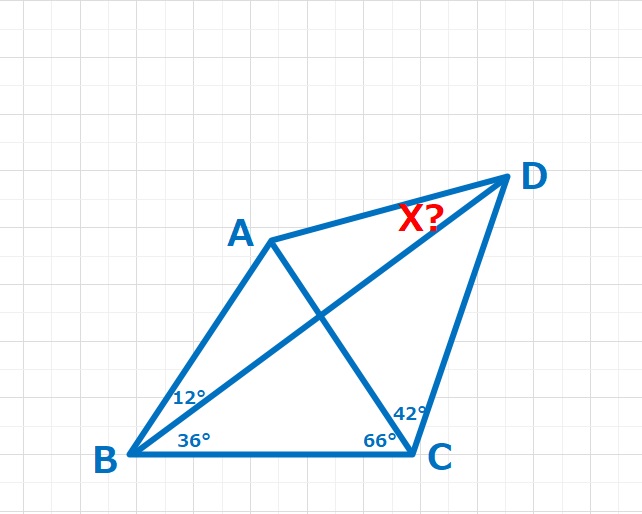 角度の問題
角度の問題 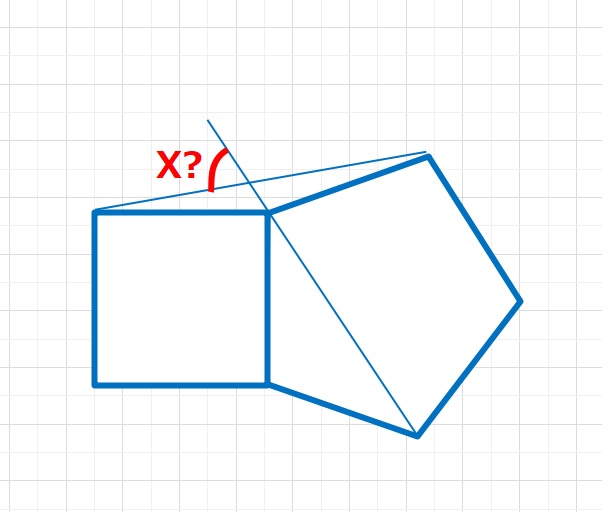 角度の問題
角度の問題 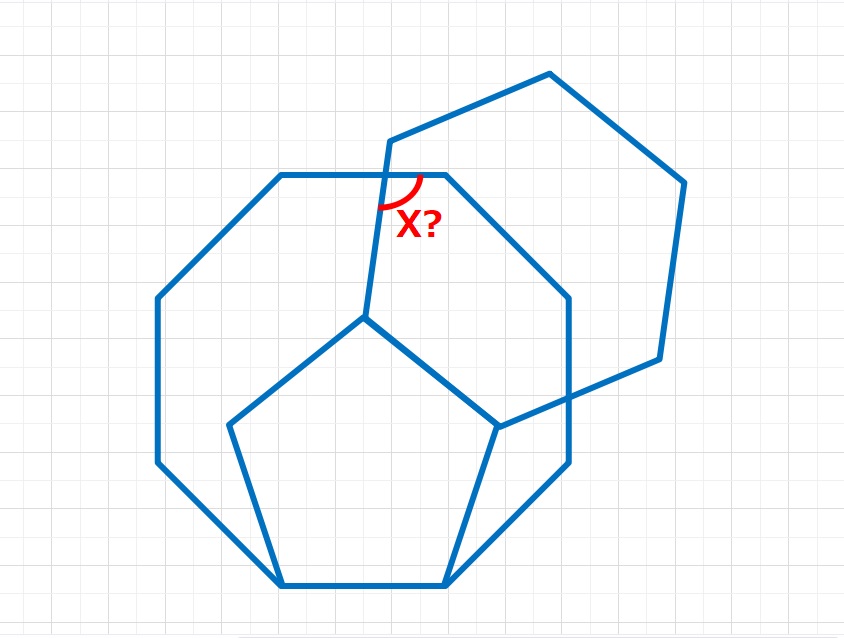 角度の問題
角度の問題 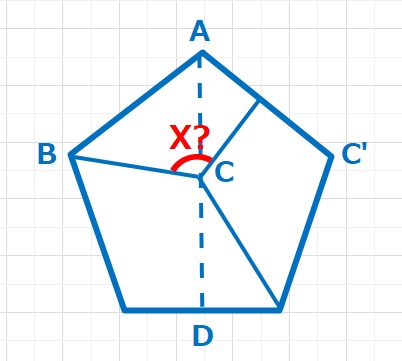 角度の問題
角度の問題 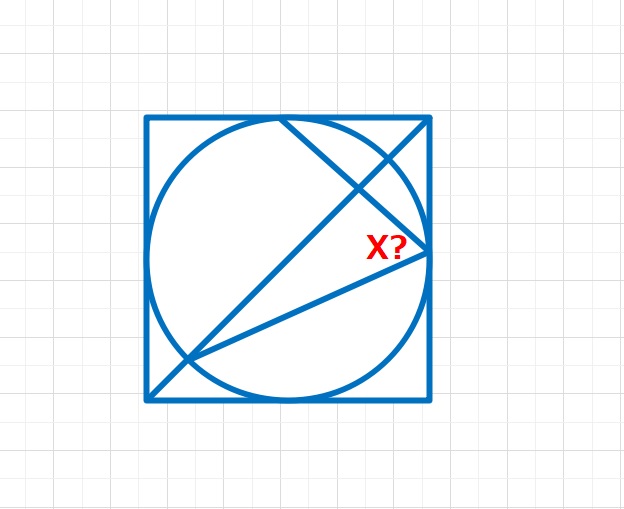 角度の問題
角度の問題