 長さ・面積・体積の問題
長さ・面積・体積の問題 ★★★☆☆難関コース パズル的思考を問う問題
2006年 東海中学入試問題より
【問題】 ブルーの3つの三角形は正三角形です。アの面積はいくつですか。
【ヒント】 3つの正三角形をぬく...
 長さ・面積・体積の問題
長さ・面積・体積の問題  長さ・面積・体積の問題
長さ・面積・体積の問題  長さ・面積・体積の問題
長さ・面積・体積の問題  長さ・面積・体積の問題
長さ・面積・体積の問題  長さ・面積・体積の問題
長さ・面積・体積の問題 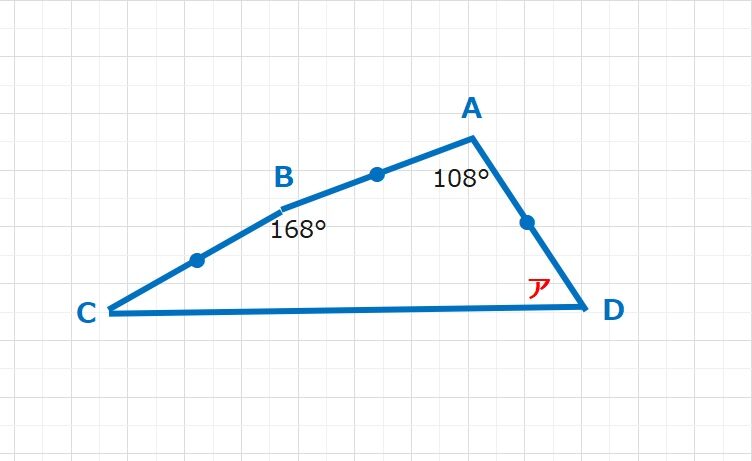 角度の問題
角度の問題 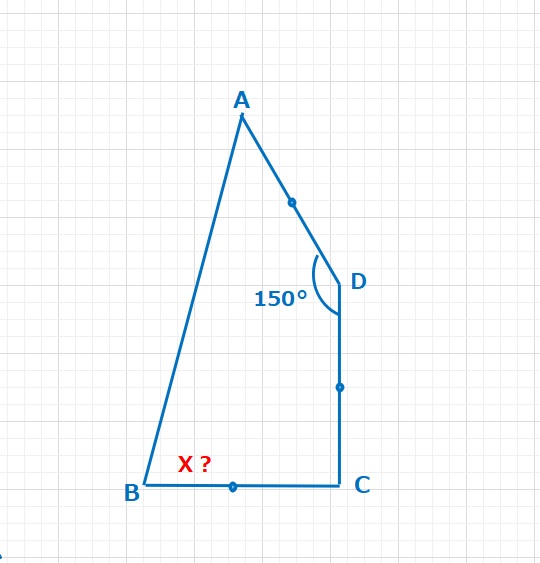 角度の問題
角度の問題 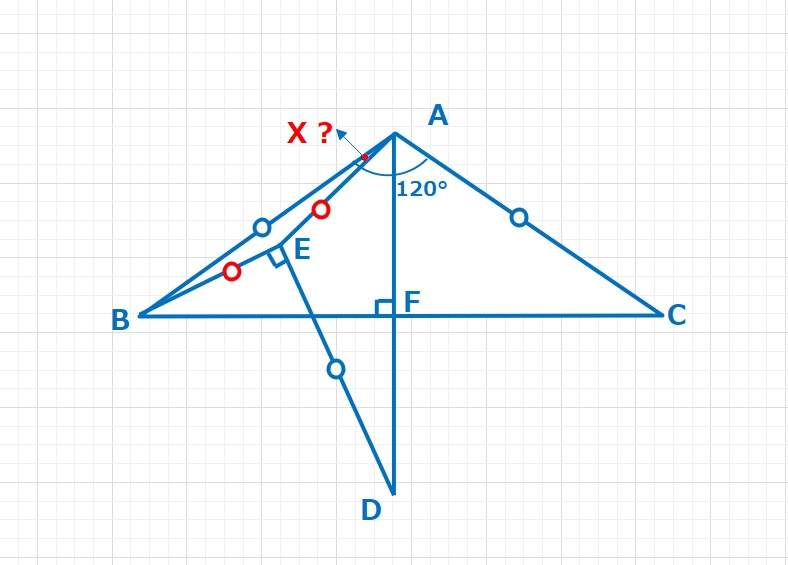 図形
図形 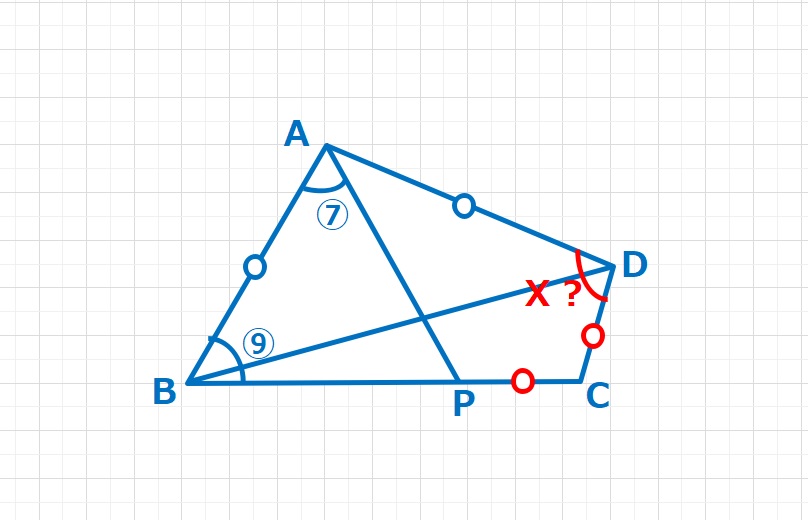 図形
図形 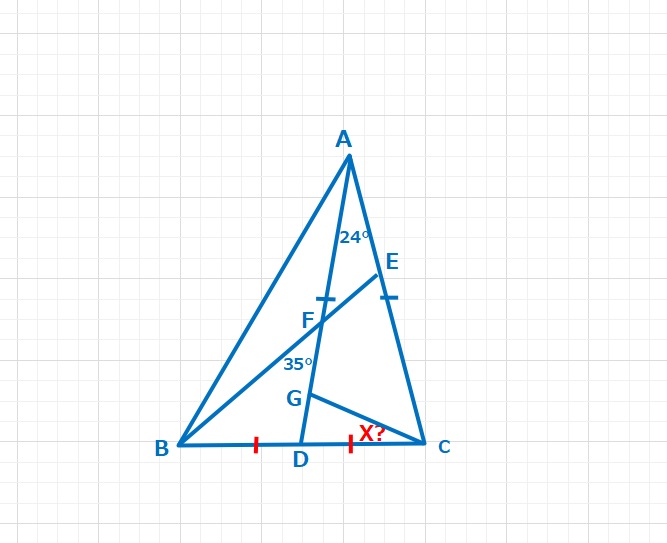 図形
図形 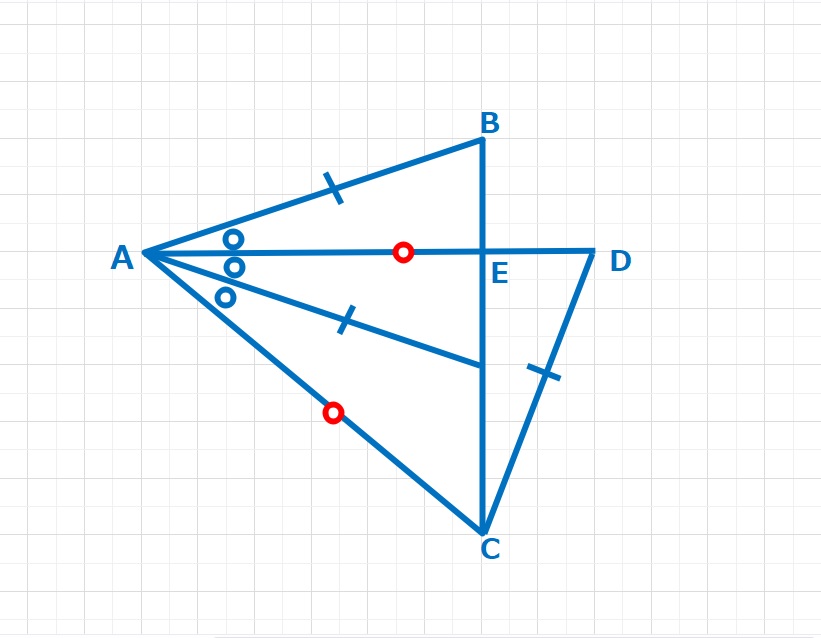 図形
図形 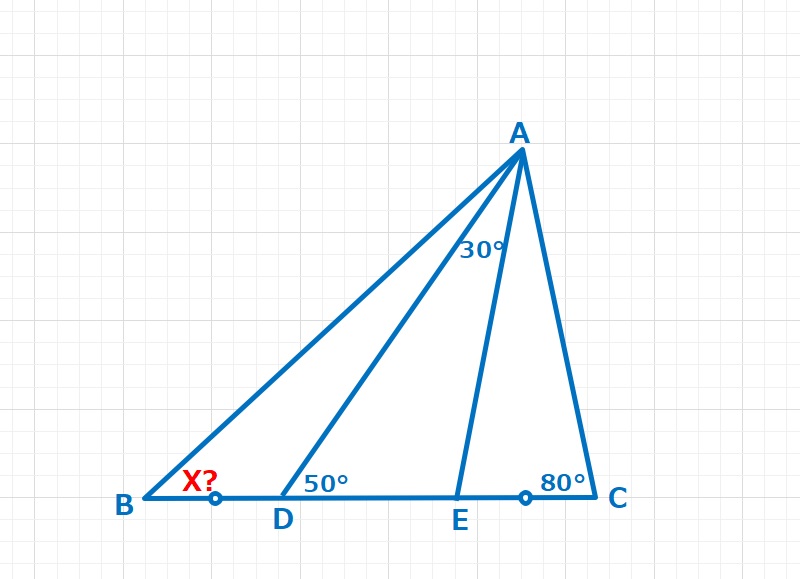 図形
図形 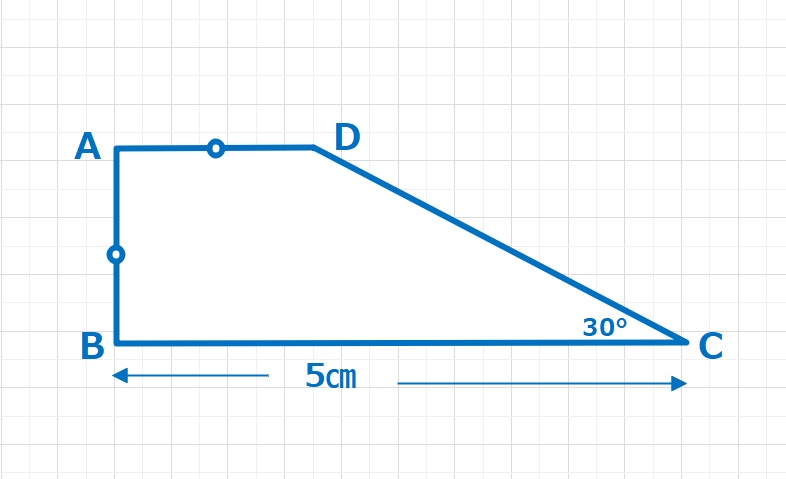 図形
図形 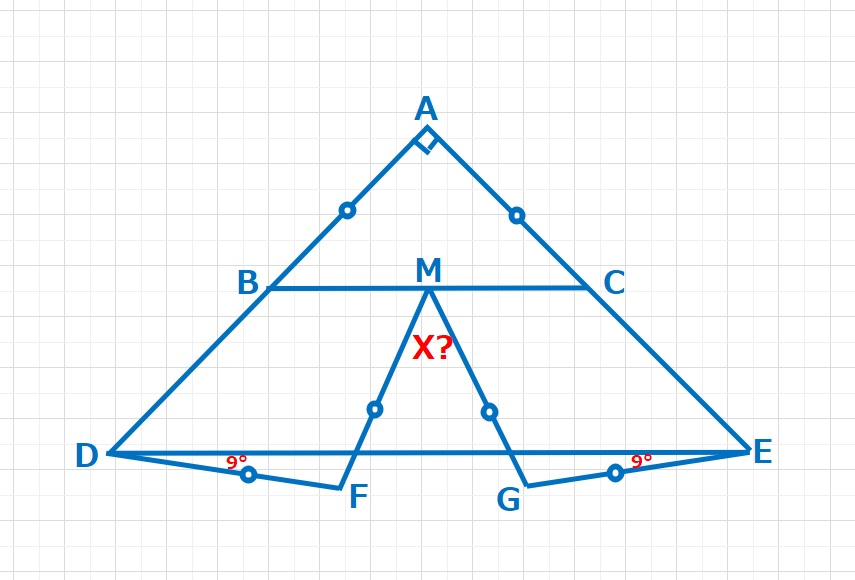 図形
図形 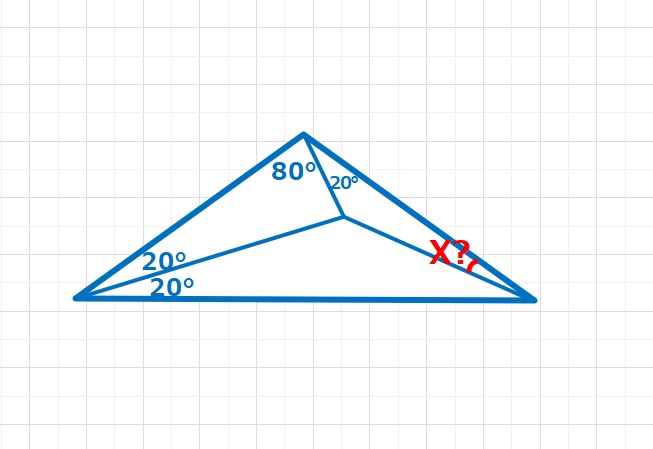 角度の問題
角度の問題 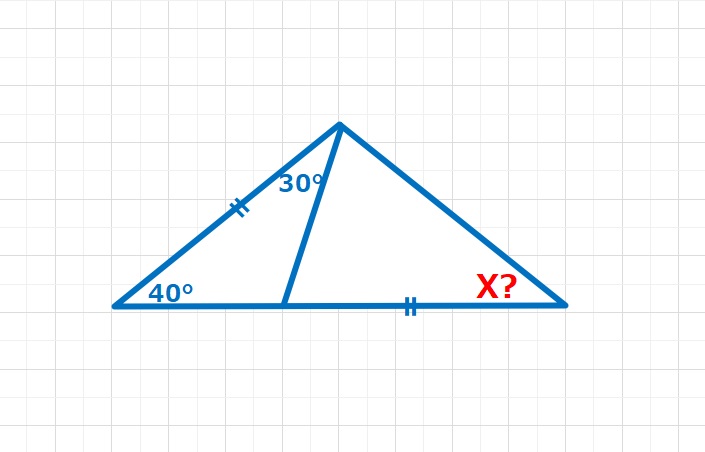 図形
図形 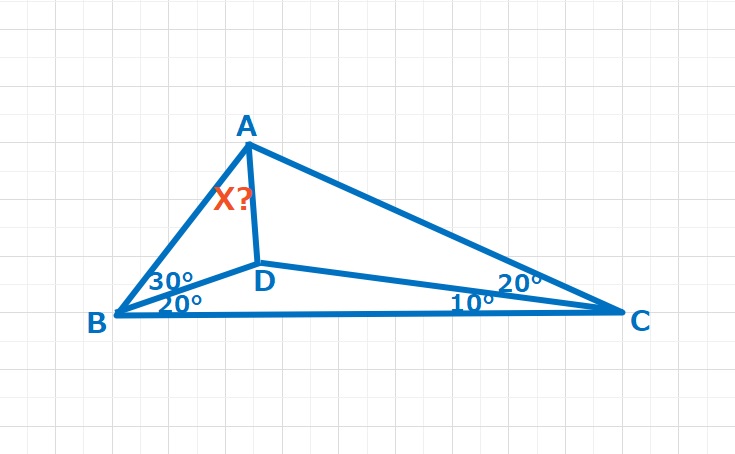 ラングレーの問題
ラングレーの問題 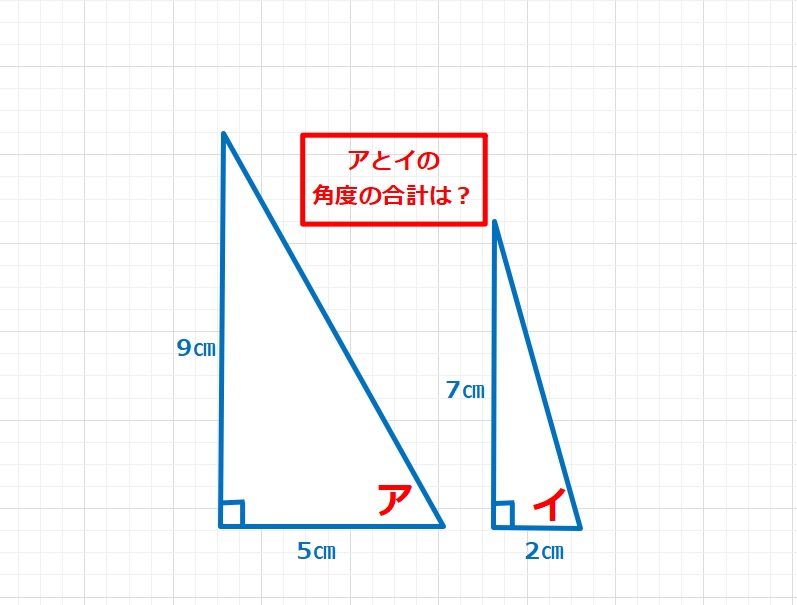 図形
図形