 図形
図形 ★★★☆☆難関コース 算数オリンピック出題問題 シンメトリー(対象)を大事にする。
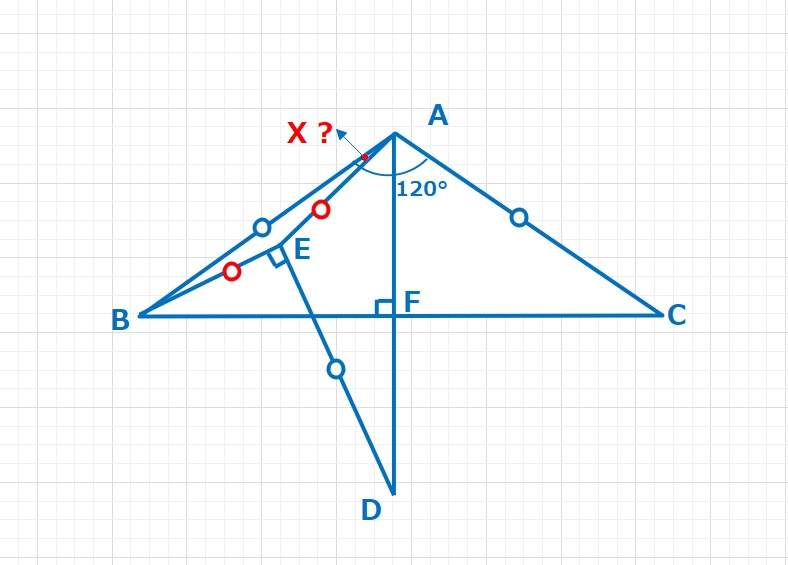
難易度2013年 算数オリンピック トライアル問題【問題】図において、AB=AC=ED, AE=BE,∠CAB=120°,∠AFC=∠BED=90°であるとき、X=∠BFEの大きさは何度ですか。
【ヒント1】左半分で十分なは...
 図形
図形  図形
図形  図形
図形  図形
図形 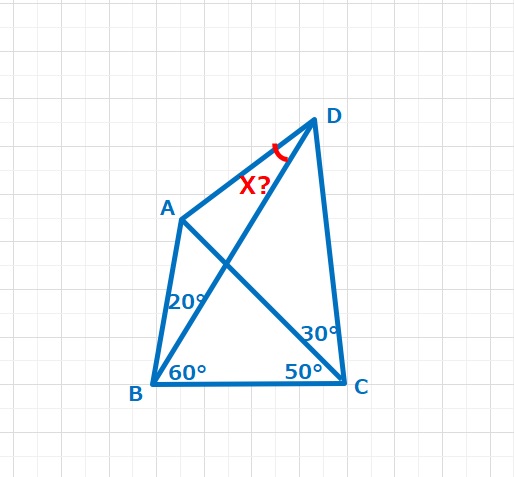 ラングレーの問題
ラングレーの問題 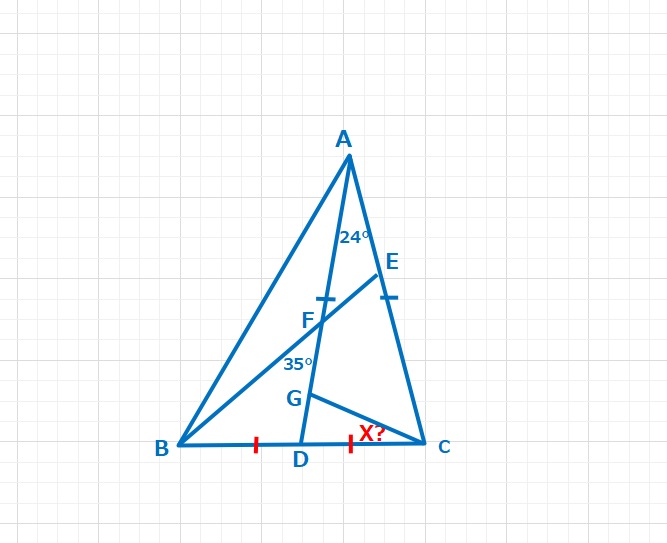 図形
図形 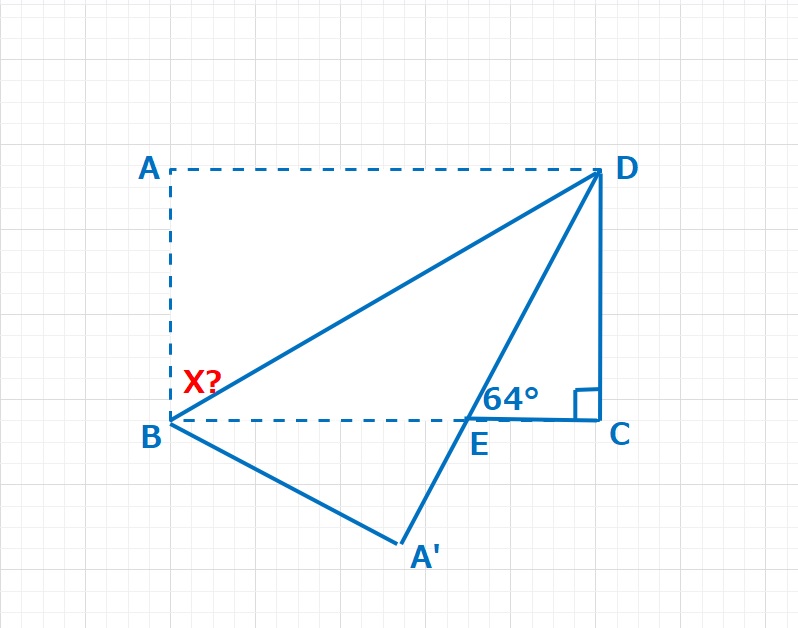 図形
図形 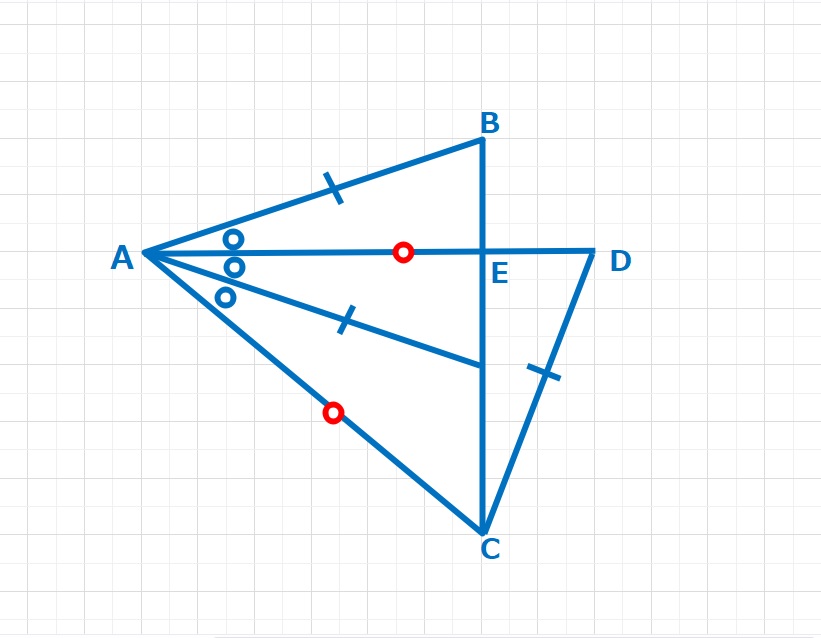 図形
図形 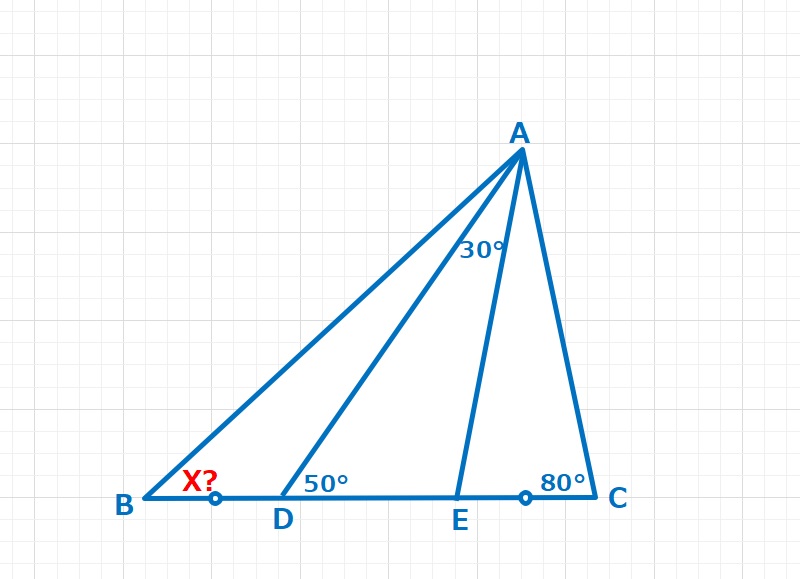 図形
図形 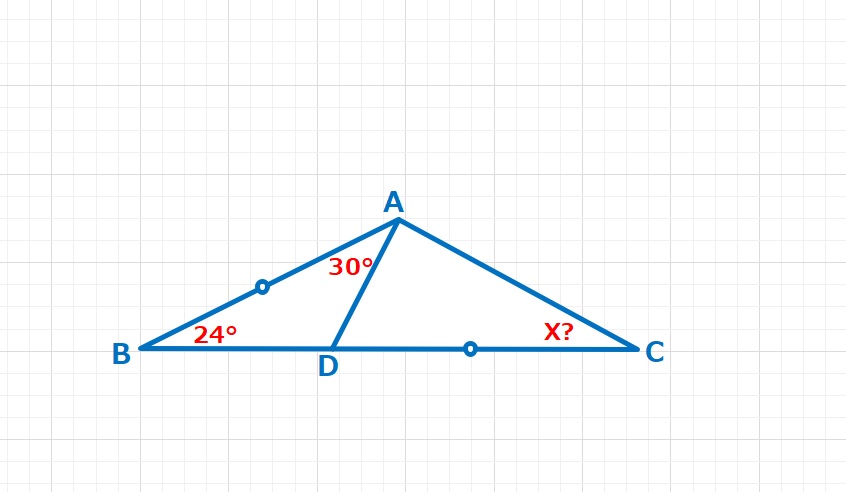 図形
図形 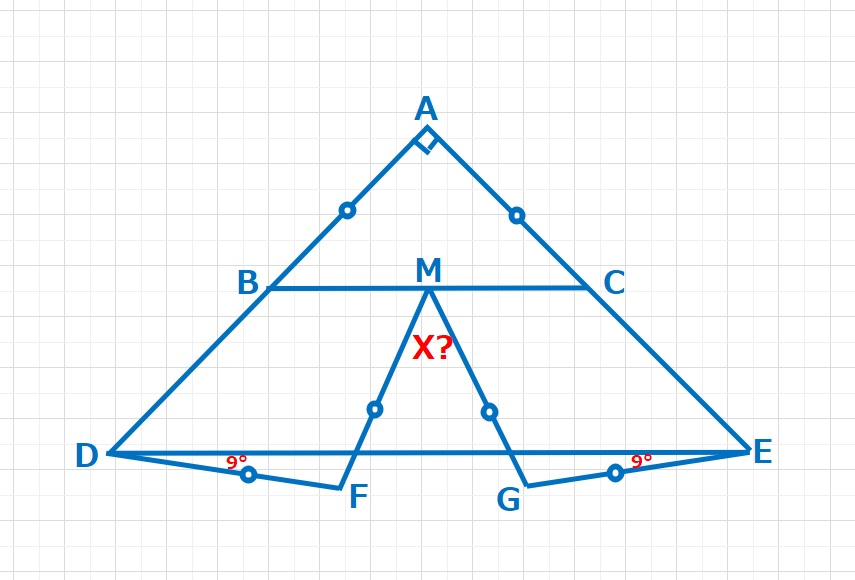 図形
図形 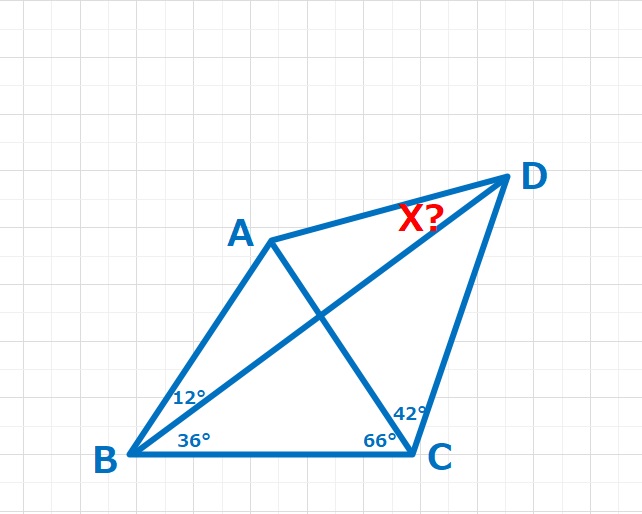 角度の問題
角度の問題 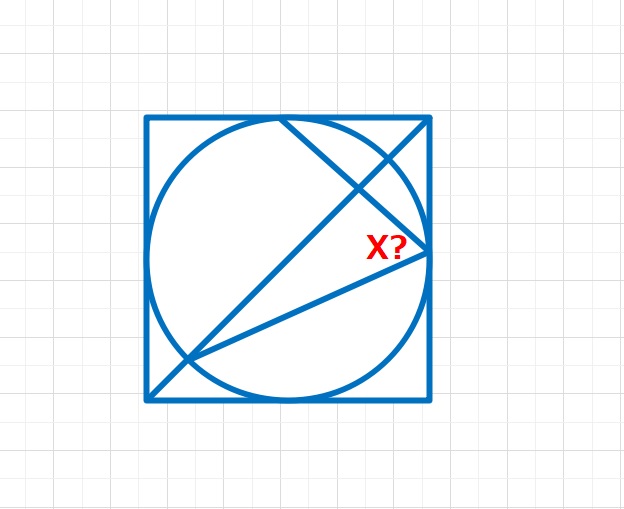 角度の問題
角度の問題 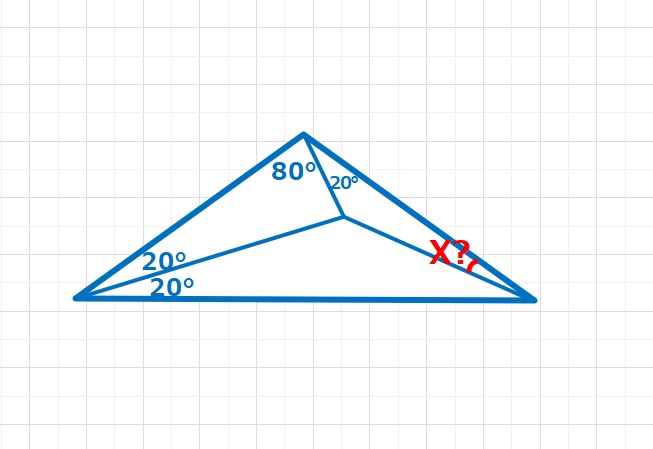 角度の問題
角度の問題 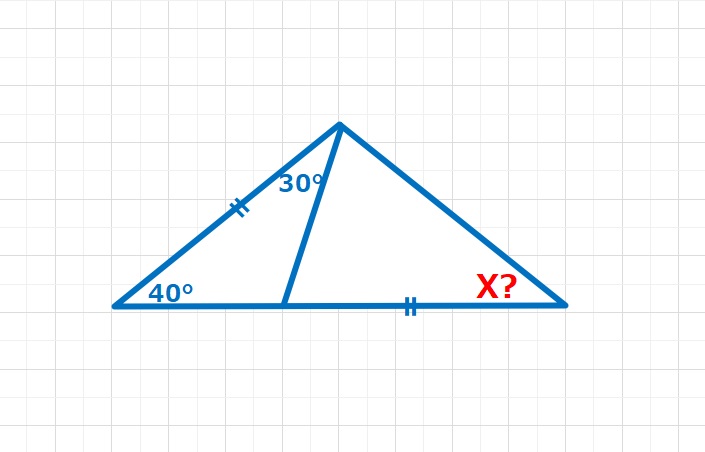 図形
図形 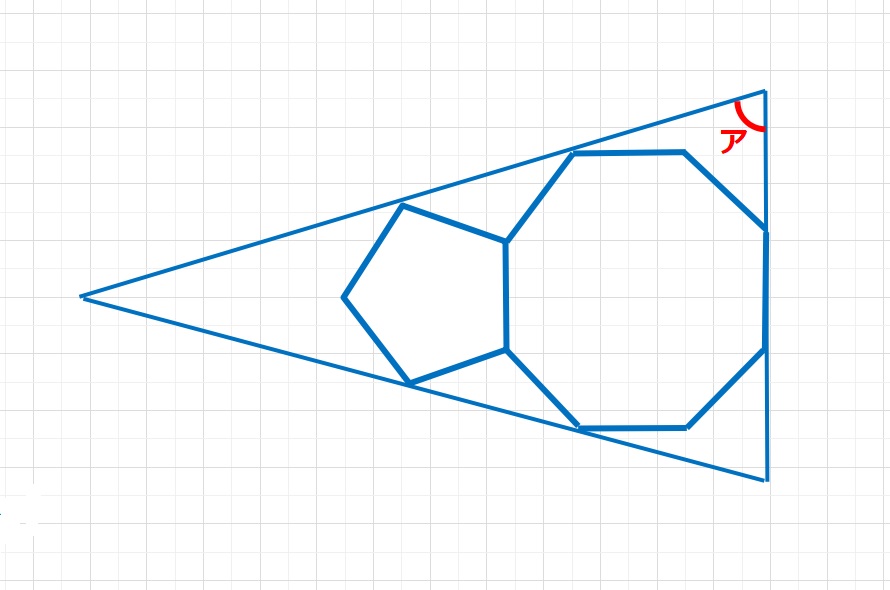 図形
図形 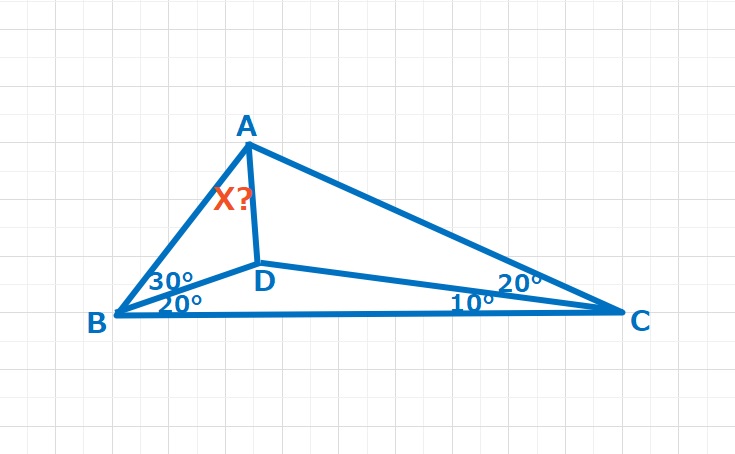 ラングレーの問題
ラングレーの問題 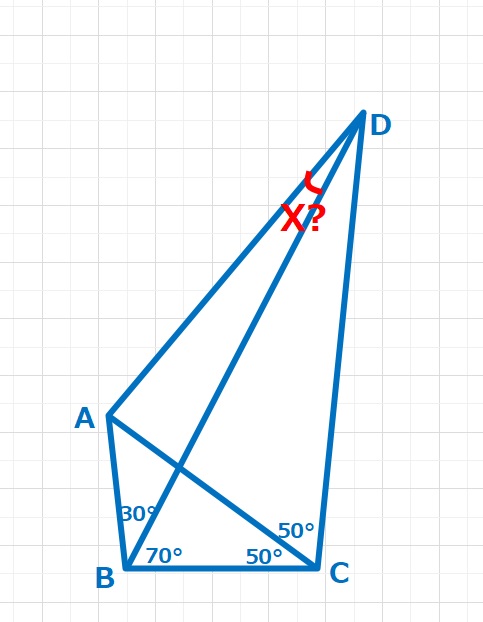 ラングレーの問題
ラングレーの問題 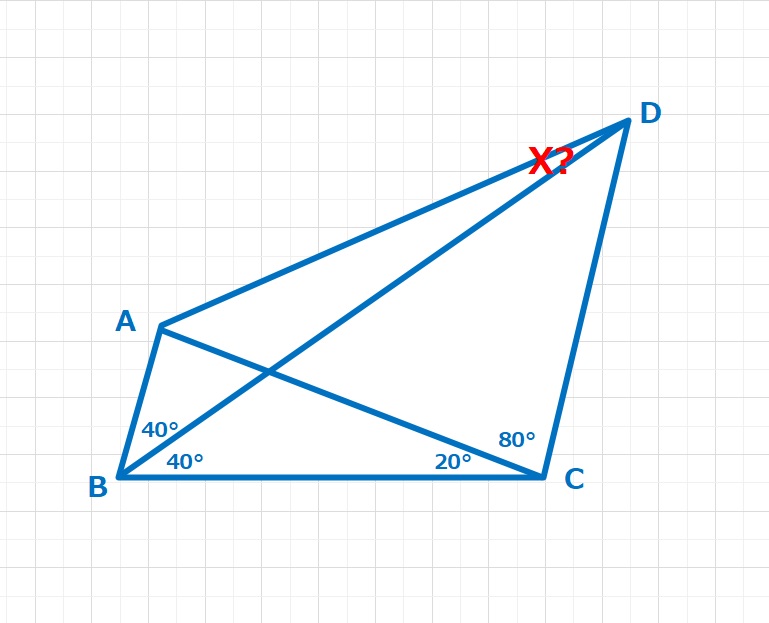 ラングレーの問題
ラングレーの問題 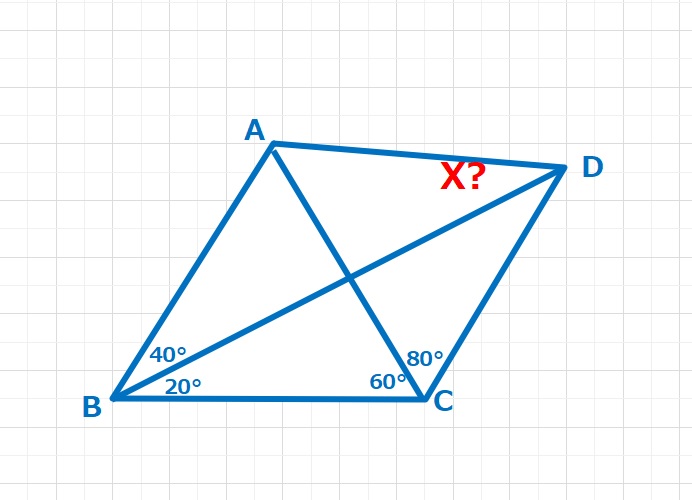 ラングレーの問題
ラングレーの問題