 図形
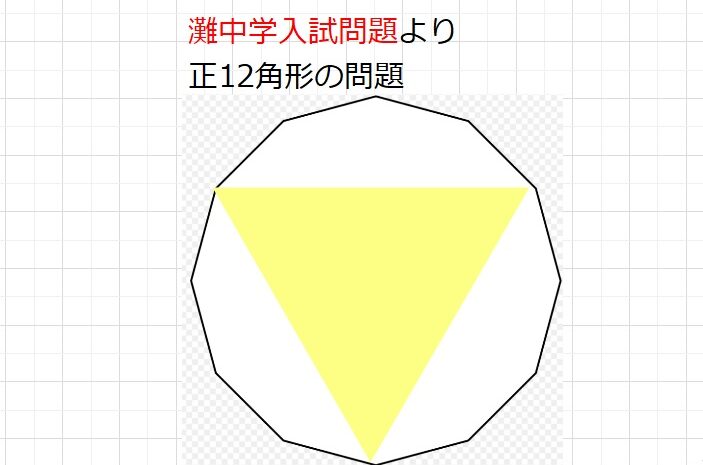
図形 ★★★☆☆難関コース 正12角形の問題 灘中入試問題より
灘中学 2022年入試問題よりこの問題、絶対に解いてほしい問題です。とてもよくできていると思います。是非なんどもなんども自分のものになるまで解いてください。【問題】図のように1辺の長さが1cmの正12角形があります。この正12角形の面積は...
 図形
図形 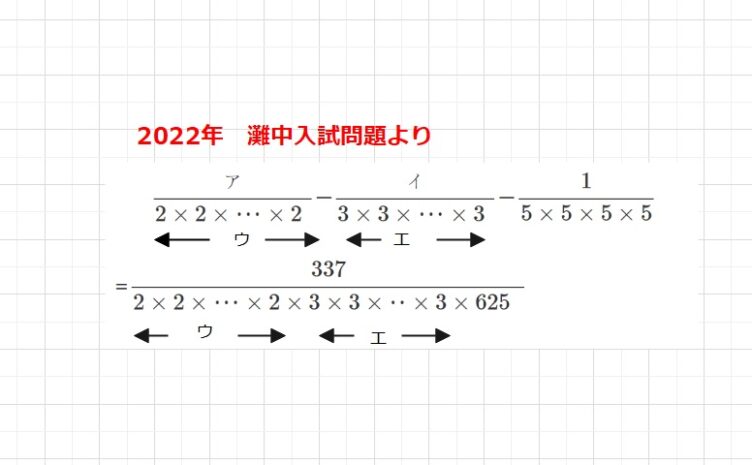 数と計算
数と計算  偶数・奇数・倍数・約数
偶数・奇数・倍数・約数  場合の数
場合の数  わり算(除法)
わり算(除法)  1行計算問題・文字を使った式
1行計算問題・文字を使った式  偶数・奇数・倍数・約数
偶数・奇数・倍数・約数  1行計算問題・文字を使った式
1行計算問題・文字を使った式 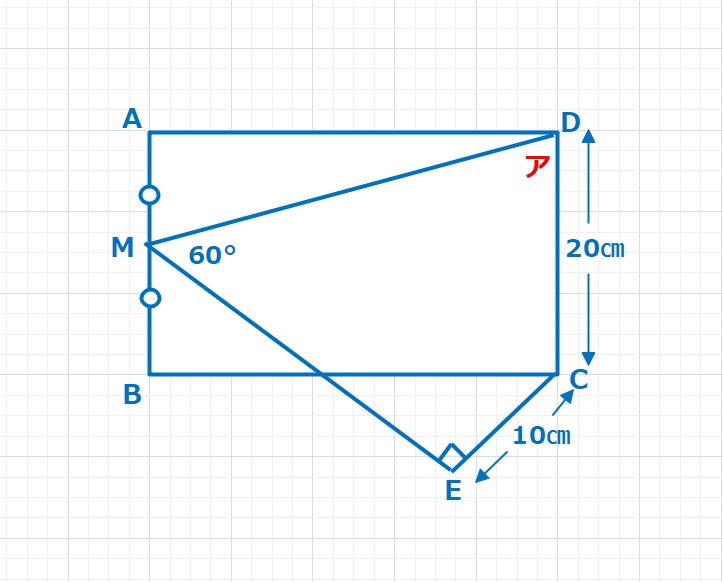 図形
図形 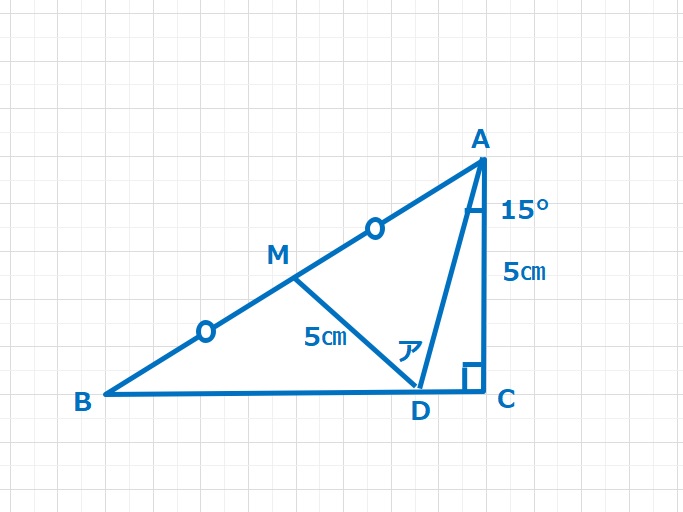 図形
図形 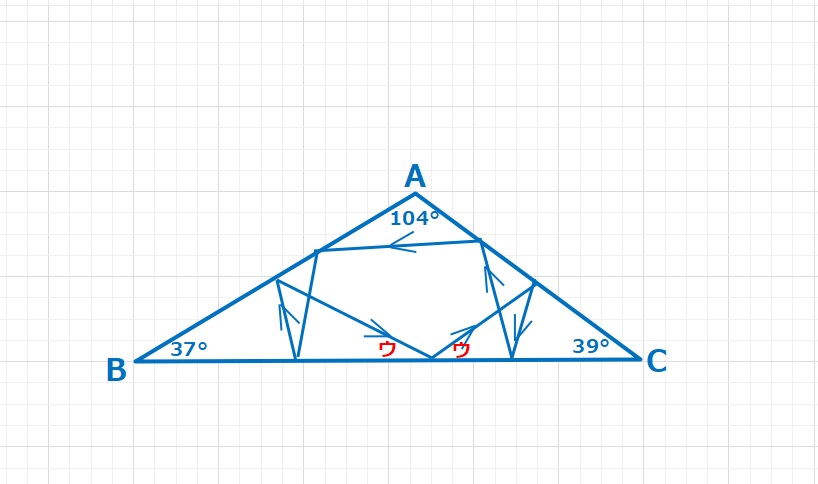 図形
図形 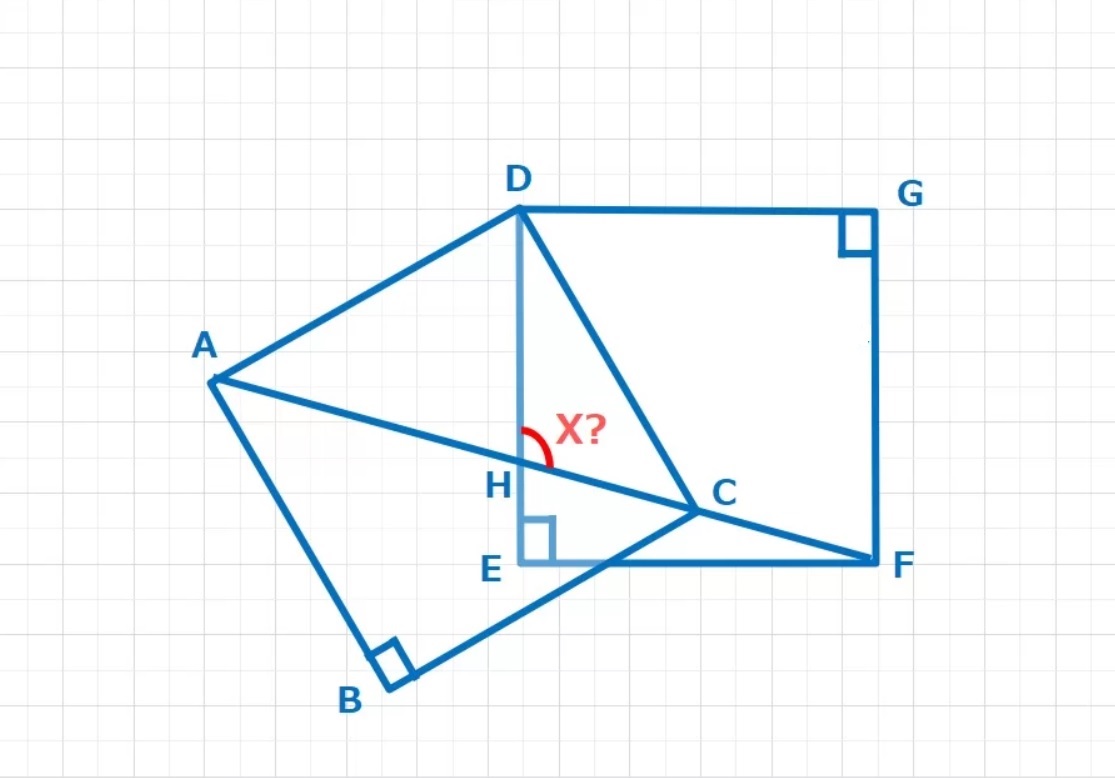 図形
図形 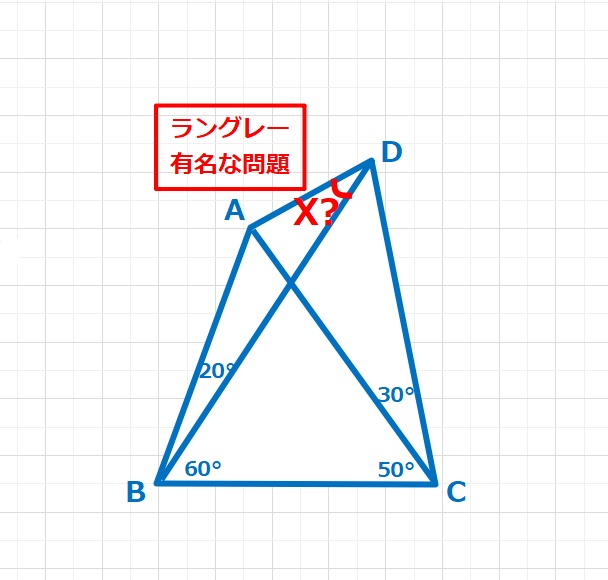 ラングレーの問題
ラングレーの問題